Techniques d'échantillonnages:

EXEMPLE1 :
Supposons que l’on doive choisir un échantillon aléatoire simple de 5 unités dans une liste de 40 unités numérotées en série, que l’on consulte l’Annexe 6 : Table de nombres aléatoires et que l’on choisisse dans la colonne 5) des nombres à deux chiffres les nombres suivants :
39, 27, 00, 74, 07
Pour donner les mêmes probabilités de sélection aux 100 unités, il faut rejeter tous les nombres supérieurs à 79 et considérer que (00) équivaut à 80. Ensuite, on divise les nombres ci-dessus par 40, et l’on prend les restes comme numéros des bandes sélectionnées pour l’échantillon, en rejetant les restes qui sont répétés. On obtient ainsi les 16 numéros de bande comme échantillon, soit : 39, 27, 40, 34, 7.
2. Estimation de paramètres
Soient y1, y2,… ,yn les mesures d’une caractéristique spécifique, effectuées sur n unités sélectionnées d’un échantillon d’une population de N unités

 d’échantillonnage. On constate dans le cas d’un échantillonnage aléatoire simple sans remise que la moyenne de l’échantillon

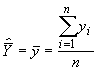
est un estimateur non biaisé de la moyenne de la population. Une estimation non biaisée de la variance d’échantillonnage de est donnée par

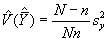
ou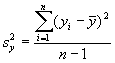

Si l’estimation y suit une loi normale, il est possible d’établir un intervalle de confiance sur la moyenne de la population , les limites de confiance inférieure et supérieure étant définies par,

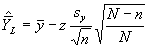  Limite inférieure

Limite supérieure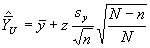  

où z est la valeur de la table qui dépend du nombre d’observations incluses dans l’échantillon. Si leur nombre est égal ou supérieure à 30, on peut extraire ces valeurs de la table de la distribution normale (Annexe 1). Si le nombre d’observations est inférieur à 30, la valeur tabulaire sera extraite de la table de distribution t (Annexe 2), avec n - 1 degrés de liberté.
Nous allons illustrer ces calculs par un exemple. Supposons qu’une forêt ait été divisée en 1000 parcelles de 0,1 hectare chacune et qu’un échantillon aléatoire simple de 25 parcelles ait été selectionné. Pour chacune de ces parcelles d’échantillon, les volumes de bois, en m3, ont été enregistrés. Ces volumes étaient les suivants:
7 10 7 4 7
8 8 8 7 5
2 6 9 7 8
6 7 11 8 8
7 3 8 7 7
Si le volume de bois de la i-ème unit d’échantillonnage est noté yi, un estimateur non biaisé de la moyenne de la population, s’obtient à l’aide de l’Equation (5.11), soit :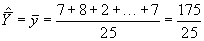 =7

qui est le volume moyen de bois par parcelle de 0.1 ha , dans la superficie de forêt.
Une estimation () de la variance des valeurs individuelles de y s’obtient à l’aide de l’équation (5.13).

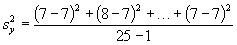=3.833

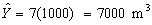
L’intervalle de confiance de 95% associé à la moyenne de la population est de (6.20, 7.80) m3. Cela signifie que l’on peut estimer qu’il y a 95 chances sur cent que l’intervalle de confiance de (6.20, 7.80) m3 inclura la moyenne de la population.
On obtiendra facilement une estimation du volume total de bois dans la surface de forêt échantillonnée en multipliant l’estimation de la moyenne par le nombre total de parcelles comprises dans la population. Ainsi
avec une intervalle de confiance de (6200, 7800) obtenu en multipliant les limites de confiance associés à la moyenne par N = 1000. L’erreur-type relative RSE de , n’est cependant pas modifiée par cette opération.