1. Limites de la logique du 1er ordre. 1
5. Truth maintenance system(TMS) 4
1. Limites de la logique du 1er ordre
La logique formelle (propositionnelle et logique de 1er ordre) ont des limitations et ne peuvent pas être appliquées directement pour résoudre des problèmes réels. La résolution des problèmes en utilisant la logique consiste à les formuler comme un problème de preuve de théorème en utilisant par exemple la procédure (résolution).
La logique de proposition et sound, complète et décidable
La logique des prédicat est sound , complète et semi-décidable
Le raisonnement basé sur la procédure de résolution utilisé pour prouver un théorème est intractable. Ce qui rend l’utilisation de la logique pour résoudre des problème réels large impraticable.
Une solution était :
Améliorer l’efficience de la procédure en
1)sacrifiant la propriété(s) soundness et /ou completeness de la logique .
2) diminuer l’expressivité du langage. Par exemple l’utilisation du langage basé sur les clauses de horn.
Le raisonnement est plus efficace avec les clauses de horn et peut être met en pratique pour résoudre des problèmes réels.
Une autre limitation est que le modèle suppose que la KB est complète, consistante et certaine. On a supposé qu’une quantité reliable de connaissance est présente (faits, règles..etc) pour déduire des conclusions certaines. Cette forme de raisonnement est importante mais a des limitations :
La connaissance réelle est souvent incertaine, vague, ambigüe, imprécise, supposée.
La logique classique ne fournit pas un formalisme adapté au problèmes réels ou la connaissance n’est pas de nature booléenne.
Mais les humains n’ont pas de difficulté et raisonnent même dans ces conditions.
Plusieurs approches ont été proposée pour satisfaire cet objectif( fuzzy logic, raisonnement bayesien…).
Une autre faiblesse de la logique des prédicats et du raisonnement déductif est que les bases de connaissances et Les techniques de l'inférence ne produiront jamais de nouvelles connaissances sur le monde, elles convertissent simplement les connaissances implicites en connaissances explicites en utilisant la déduction.
Les humains utilisent souvent le raisonnement analogique et inductif pour acquérir de nouvelles
connaissance. Dans le raisonnement analogique, un problème est résolu en adoptant une solution d'un problème similaire, déjà résolu et dans l’ inductif le raisonnement traite la dérivation de connaissances généralisées sur les domaine du problème à partir d'un ensemble d'instances ou d'observations.
La logique de premier ordre est monotone. Mais les humains appliquent un raisonnement non-monotone.
Par exemple, vous savez peut-être que les chiens aiment manger de la viande et que Fido est un chien. Par conséquent, vous concluez que Fido aimera manger de la viande. Si vous apprenez plus tard que Fido est un chien végétarien, vous devrez modifier votre conclusion. Ce type de raisonnement est appelé raisonnement non monotone.
2. Raisonnement monotone
Un système logique est décrit comme étant monotone si une preuve valide dans le système ne peut pas être invalidée en ajoutant des prémisses ou des hypothèses supplémentaires.
En d'autres termes, si nous constatons que nous pouvons prouver une conclusion C en appliquant des règles de déduction à une prémisse B avec des hypothèses A, alors l'ajout d'hypothèses supplémentaires A1 et B1 ne nous empêchera pas de pouvoir déduire C même si A1 et B1 rend le système inconsistant
La monotonie d'un système logique peut être exprimée comme suit :
If we can prove {A, B} |- C, then we can also prove: {A, B, A1, B1} |- C.
Noter que A1 et B1 peuvent être n’importe quoi (même la négation de A et la négation de B).
En d'autres termes, un système de raisonnement monotone qui stocke des faits sur le monde peut déduire de nouveaux faits de ses faits existants mais n'aurait jamais de raison de supprimer ou de modifier un fait existant (à moins que le monde ne change pas ).
Par conséquent, le nombre de faits que le système stocke augmentera de manière monotone.
Dans la vraie vie, le raisonnement (humain) a tendance à ne pas être aussi simple. Par exemple, vous savez peut-être que les chiens aiment manger de la viande et que Fido est un chien. Par conséquent, vous concluez que Fido aimera manger de la viande. Si vous apprenez plus tard que Fido est un chien végétarien, vous devrez modifier votre conclusion. Ce type de raisonnement est appelé raisonnement non monotone.
Un système de raisonnement non monotone doit être capable de gérer le fait que les conclusions changent à mesure que de nouveaux faits sont introduits et par conséquent que sa connaissance n'est pas toujours certaine car des faits ultérieurs peuvent la contredire. Dans ce contexte, nous utilisons souvent le mot « croyance » plutôt que « fait » pour décrire des éléments de données que le système stocke ou déduit sur le monde.
La suite présente des systèmes et des principes pour traiter le raisonnement non-monotone.
3. Default Reasoning
Le raisonnement par défaut est une autre forme de raisonnement non monotone qui implique de supposer que certaines déclarations sont vraies, à moins qu'il n'y ait une preuve claire du contraire. C'est une forme de raisonnement que les gens emploient tout le temps. Par exemple, une voiture peut vous dépasser trop vite pour que vous puissiez voir si elle a un chauffeur ou non. Il serait raisonnable pour vous de supposer que la voiture a un conducteur, à moins que vous ne sachiez qu'il s'agit d'une voiture télécommandée ou que vous ayez vu le conducteur sauter précédemment. C'est le raisonnement par défaut, car il suppose certains faits par défaut, à moins qu'ils ne soient réfutés par d'autres faits.
4. Closed-World Assumption
Une autre forme d'hypothèse, faite à l'égard des connaissances incomplètes, est de nature plus globale que les défauts uniques.
La notion d'hypothèse de monde clos est utilisée en particulier en Prolog, L' hypothèse du monde fermé (également connue sous le nom de négation par échec ) est une hypothèse utilisée par les systèmes selon laquelle tout fait qui n'est pas spécifiquement connu pour être vrai n'est pas vrai. Par exemple, si un système utilise une base de données de faits et qu'un fait particulier n'est pas inclus dans la base de données, alors ce fait est supposé être faux.
Donc Cela signifie que dans une KB si le littéral P(a) est non prouvable, alors not P(a) est supposée vérifiée.
En augmentant une KB avec une hypothèse (une metaregle) qui stipule que si l'atome groud P(a) ne peut pas être prouvé, supposons sa négation not P(a), le CWA complète la théorie par rapport à KB. (Rappelons qu'un Système formel est complet si et seulement si chaque atome ground ou sa négation est dans le système.)
Mais
En général, une KB augmenté de CWA n'est pas cohérente. Cela se voit facilement en considérant la KB formée de la clause
P(a) V Q(b)
Maintenant, puisqu'aucun des littéraux grounds de cette clause n'est dérivable, la KB augmentée devient
P(a) V Q(b)
Not P(a),not Q(b) ce montre qu’elle est incohérente.
On peut montrer que la cohérence peut être maintenue pour un type particulier de CWA. Il s'agit d'un KB composée de clauses de Horn. Si une KB est cohérente et horn, son augmentation CWA est cohérente. (Rappelez-vous que les clauses de Horn sont des clauses avec au plus un littéral positif.)
Un système logique utilisant l'hypothèse du monde fermé devient non monotone. Étant donné une base de connaissances D avec une formule atomique h non complétant D, (donc sous CWA, h est faux), il est possible que, lorsque la base de connaissances est augmentée de nouveaux faits ou règles (non simplement déductibles de la connaissance base), alors on peut prouver que h est vrai
5. Truth maintenance system(TMS)
Nous commençons dans la section suivante par une description des systèmes de maintien de la vérité (TMS). Un TMS est un système mise en place pour permettre une forme de raisonnement non monotone en permettant l'ajout d'énoncés changeants (même contradictoires) à une base de connaissances.
Les systèmes de maintien de la vérité (également connus sous le nom de systèmes de révision de croyance) sont des composants complémentaires aux systèmes d'inférence. Le travail principal du TMS est de maintenir la cohérence des connaissances utilisées par le résolveur de problèmes et non pas pour effectuer des fonctions d'inférence. En tant que tel, il libère le résolveur de problèmes de tout souci de cohérence et lui permet de se concentrer sur la solution du problème.
Le TMS donne également au composant d'inférence la capacité nécessaire pour effectuer des inférences non monotones. Lorsque de nouvelles découvertes sont faites, ces informations plus récentes peuvent remplacer des conclusions antérieures qui ne sont plus valables. De cette façon, l'ensemble des croyances disponibles pour le résolveur de problèmes continuera d'être actuel et cohérent.
La figure suivante montre la relation entre tms et ie et KB.
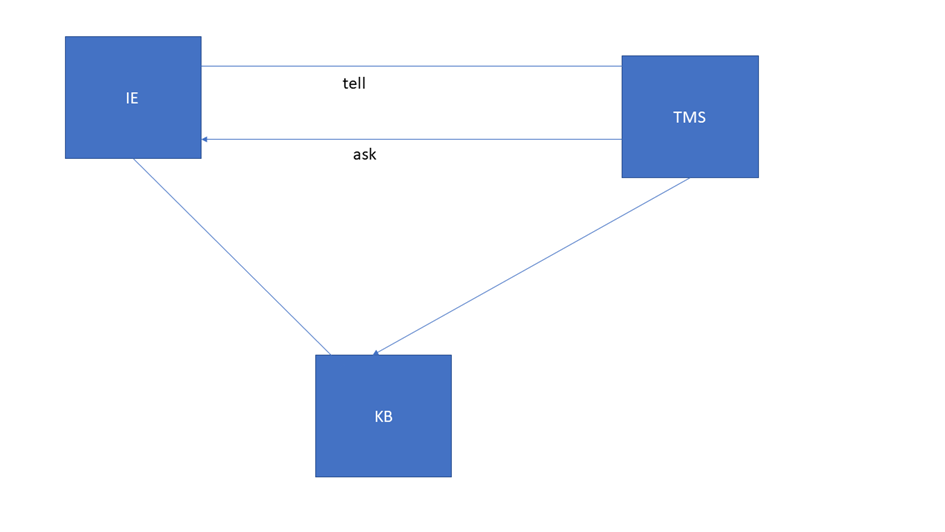
Le moteur d'inférence (IE) résout les problèmes de domaine en fonction de son ensemble de croyances actuel, tandis que le TMS maintient l'ensemble de croyances actuellement actif. Le processus de mise à jour est incrémental. Après chaque inférence, des informations sont échangées entre les deux composants.
L'IE indique au TMS les déductions qu'il a effectuées. Le TMS, à son tour, pose des questions sur les croyances actuelles et les raisons des échecs. Il maintient un ensemble cohérent de croyances avec lesquelles l'IE peut travailler même si de nouvelles connaissances sont ajoutées et supprimées.
Exemple
Supposons que la base de connaissances (KB) ne contienne que les propositions
P, P=>Q, et modus ponens. À partir de là, l'IE infère Q et ajouterait cette conclusion à la base de connaissances. Plus tard, si l'on apprenait que not P était approprié, il serait ajoutée au KB, ce qui entraînerait une contradiction. Par conséquent, il faudrait supprimer P pour éliminer l'incohérence. Mais, avec P maintenant supprimée, Q n'est plus une croyance justifiée. Il devrait également être supprimé. Ce type de révision des croyances est le travail du TMS.
Approche simple de maintenance de la vérité
Une approche simple du maintien de la vérité consiste à suivre l'ordre dans lequel les phrases sont transmises à la base de connaissances en les numérotant de P1 à Pn. Quand l'appel RETRACT(KB, Pi) est effectué, le système revient à l'état juste avant l'ajout de Pi, supprimant ainsi à la fois Pi et toutes les inférences dérivées de Pi. Les phrases Pi+1 à Pn peuvent alors être ajoutées à nouveau. C'est simple et cela garantit que la consistance de la base de connaissances , mais rétracter Pi nécessite de rétracter et de réaffirmer n − i phrases ainsi que de défaire et de refaire toutes les inférences tirées de ces phrases. Pour les systèmes auxquels de nombreux faits sont ajoutés, tels que les grandes bases de données commerciales, cela n'est pas pratique.
JTMS (justification-based truth maintenance)
Une approche plus efficace est le système de maintien de la vérité basé sur la justification, ou JTMS.
La JUSTIFICATION Dans un JTM : chaque phrase de la base de connaissances est annotée d'une justification constituée de l'ensemble des phrases à partir desquelles elle a été déduite. Par exemple, si la base de connaissances contient déjà P ⇒ Q, alors TELL(P) fera ajouter Q avec la justification {P, P ⇒ Q}. En général, une phrase peut avoir n'importe quel nombre de justifications. Les justifications rendent la rétractation efficace. Étant donné l'appel RETRACT(P), le JTMS supprimera exactement les phrases pour lesquelles P est un membre de chaque justification. Ainsi, si une phrase Q avait la seule justification {P, P ⇒ Q}, elle serait supprimée ; s'il avait la justification supplémentaire {P, P ∨ R ⇒ Q}, il serait toujours supprimé ; mais s'il avait aussi la justification {R, P ∨R ⇒ Q}, alors il serait épargné. De cette manière, le temps nécessaire à la rétraction de P dépend uniquement du nombre de phrases dérivées de P plutôt que du nombre d'autres phrases ajoutées depuis que P est entré dans la base de connaissances.
Le JTMS suppose que les phrases qui sont considérées une fois seront probablement considérées à nouveau, donc plutôt que de supprimer entièrement une phrase de la base de connaissances lorsqu'elle perd toutes ses justifications, nous marquons simplement la phrase comme étant hors (out) de la base de connaissances. Si une assertion suivante restaure l'une des justifications, puis nous marquons la phrase comme étant de retour(in). De cette façon, le JTMS conserve toutes les chaînes d'inférence qu'il utilise et n'a pas besoin de redériver les phrases lorsqu'une justification redevient valide.
