5. Two goals of a logic language. 2
8. Syntax of propositional logic. 3
10. La formule représente un ensemble de modèles. 4
12. L’Ajout à la base de connaissances Réduit l'ensemble de modèles. 4
14. Reduce Ask[f] and Tell[f] to satisfiability. 5
19. Soundness and completeness. 7
25. Resolution in propositional logic. 9
26. Conjunctive normal form.. 10
27. Algorithme de resolution. 10
28. Limitations de la logique propositionnelle. 11
34. Substitution et unification. 13
1. Motivation
If X1 + X2 = 10 and X1 − X2 = 4, what is X1?
Solution: recherche
Solution 2: 2X1=14 ce qui démontre le pouvoir de l’inférence logique par rapport au model checking qui cherche à trouver directement des affectations.
Search : inference par DFS,A*…
CSP: backtracking search, beam search, or variable elimination
Game: minimax …
Bayesien network: gibss sampling..
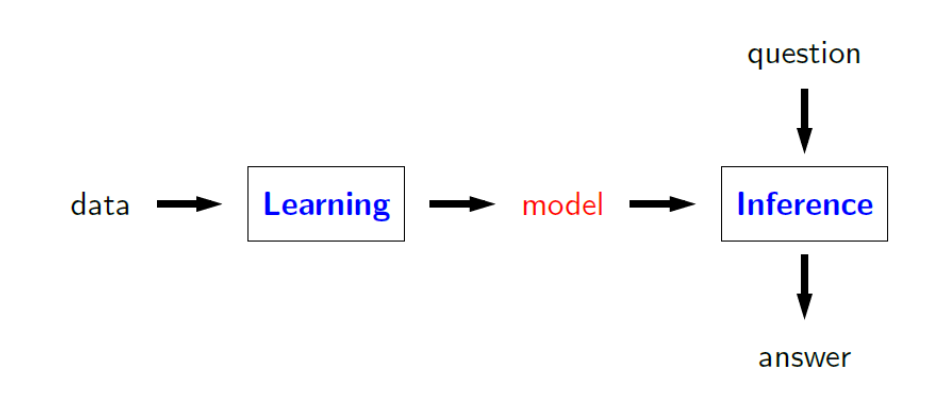
Nous pouvons considérer l'apprentissage comme une induction, où nous devons généraliser, et l'inférence comme une déduction, où il s'agit de calculer la meilleure réponse étant donnée le modele.
1. Modeling paradigms
|
Type |
inference |
exemples |
Applications: |
Think in terms |
|
|
State-based models |
as finding minimum cost paths in a graph |
search problems, MDPs, games
|
route finding, game playing, etc.
|
Think in terms of states, actions, and costs
|
|
|
Variable-based models |
as finding maximum weight assignments or computing conditional probabilities |
CSPs, Bayesian networks |
scheduling, tracking, medical diagnosis, etc. |
Think in terms of variables and factors
|
|
|
Logic-based models: |
applying a set of rules |
propositional logic, first-order logic
|
theorem proving, verification, reasoning |
Think in terms of logical formulas and inference rules
|
|
2. Logique
La logique était le paradigme dominant de l'IA avant les années 1990
mais cette approche à laisser sa place aux approches basées sur la probabilité et les approches de l'apprentissage automatique
• Problème 1 : déterministe, problème de prise en charge de l'incertitude (via la probabilité)
• Problème 2 : basé sur des règles qui ne permettait pas un réglage précis à partir des données (l'apprentissage automatique résout ce problème)
• Force : fournit de l'expressivité de manière compacte
Exemple
building smart personal assistants. • Today, we have systems like Apple’s Siri, Microsoft’s Cortana, Amazon’s Alexa, and Google Assistant.
|
--->tell |
assistant |
ß---ask |
3. Natural language
|
Example: • A dime is better than a nickel. • A nickel is better than a penny. • Therefore, a dime is better than a penny. Example: • A penny is better than nothing. • Nothing is better than world peace. • Therefore, a penny is better than world peace??? Natural language is slippery |
4. Two goals of a logic language
Represent knowledge about the world et Reason with that knowledge
Objectif de l'IA en tête : nous voulons l'utiliser pour représenter la connaissance, et nous voulons pouvoir raisonner (ou faire des inférences) avec cette connaissance.
• Enfin, nous devons garder à l'esprit que notre objectif est de faire en sorte que les ordinateurs utilisent la logique automatiquement, pas que vous le fassiez. Cela signifie que nous devons penser d’une manière mécanique.
5. Ingrédient
1) Formules
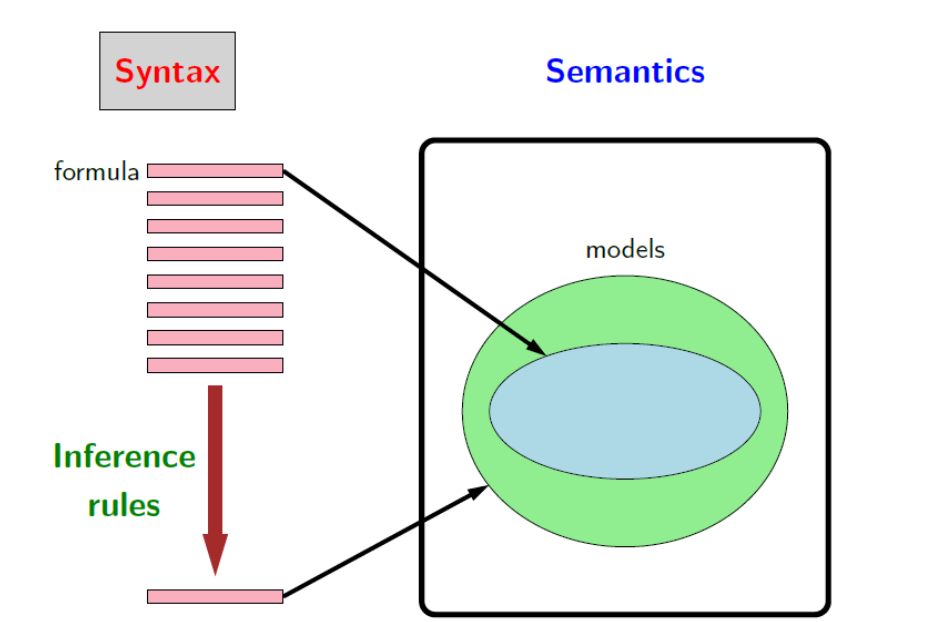
• La syntaxe définit un ensemble de formules valides,
• La sémantique ne reçoit généralement pas beaucoup d'attention si vous avez une exposition occasionnelle à la logique, mais c'est vraiment la pièce importante qui rend la logique rigoureuse. Formellement, la sémantique précise le sens d'une formule, qui dans notre cadre est un ensemble de configurations du monde dans lequel la formule est vraie. Et C'est ce qui nous importe au final.
• Mais pour y arriver, il est utile d'agir directement sur la syntaxe à l'aide d'un ensemble de règles d'inférence. Pour exemple, si je vous dis qu'il pleut et que c’est humide alors vous devriez pouvoir conclure qu'il pleut aussi (évidemment) sans même mentionner explicitement la sémantique. La plupart du temps, quand les gens font de la logique, ils ne font qu'appliquer des règles d'inférence.
6. Propositional logic
1. Syntax of propositional logic
|
(Key idea: syntax provides symbols Formulas by themselves are just symbols (syntax). No meaning yet (semantics) Propositional symbols (atomic formulas): A, B, C Logical connectives: ¬, ∧, ∨, →, ↔ Build up formulas recursively—if f and g are formulas, so are the following: • Negation: ¬f • Conjunction: f ∧ g • Disjunction: f ∨ g • Implication: f → g • Biconditional: f ↔ g |
2. semantics or meaning
|
Definition: model A model w in propositional logic is an assignment of truth values to propositional symbols. a model is a possible configuration of the world.
|
Un modèle (au sens logique) représente une situation dans le monde. En logique propositionnelle, il s'agit d'une affectation qui spécifie une valeur de vérité (vrai ou faux) pour chaque symbole propositionnel
|
Definition: interpretation function Let f be a formula. Let w be a model. An interpretation function I(f, w) returns: • true (1) (say that w satisfies f) • false (0) (say that w does not satisfy f) |
La sémantique est donnée par une fonction d'interprétation, qui prend une formule f et un modèle w, et retourne si w satisfait f. En d'autres termes, est-ce que f est vrai dans w.
3. La formule représente un ensemble de modèles
|
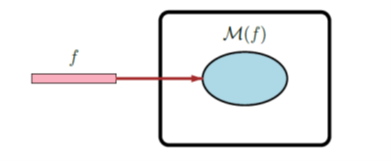
Definition: models Let M(f) be the set of models w for which I(f, w) = 1. |
|
Une façon plus utile mais équivalente de voir la sémantique est de penser la formule M(f) comme un ensemble de modèles — ceux pour lesquels I(f, w) = 1.
|
Key idea: compact representation A formula compactly represents a set of models. |
Exemple
|
Pleut et humide |
 |
1. Knowledge base
|
Une base de connaissance KB est un ensemble de formules représentant leur conjonction/intersection Intuition: KB speci_es constraints on the world. M(KB) is the set of all worlds satisfying those constraints. Each knowledge base defines a set of models — exactly those which are satisfiable by all the formulas in the knowledge base. formule= fact that you know |
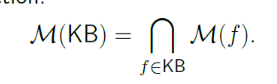 |
Exemple
|
Let KB = {pluie et neige;Traffique}.
|
|
1. L’Ajout à la base de connaissances Réduit l'ensemble de modèles
combien M(KB) diminue-t-il ? 3 cas de figures
Entailment
|
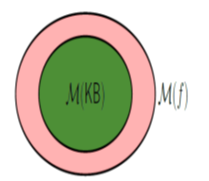
Intuition: f added no information/constraints (it was already known Example: Rain ^ Snow j= Snow |
|
Definition: entailment KB entails f (written KB |= f) iff M(KB) est inclut M(f). |
|
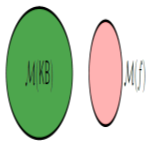
Contradiction Intuition: f contradicts what we know (captured in KB). If we believe KB, then we cannot possibly believe f. Example: Rain ^ Snow contradicts not Snow |
|
Definition: contradiction KB contradicts f iff M(KB) intersect M(f) = {};. |
|
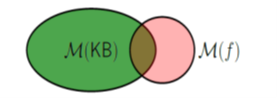
Contingency Intuition: f adds non-trivial information to KB Example: Rain and Snow |
|
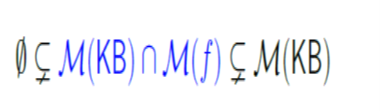 |
Proposition: contradiction and entailment KB contradicts f iff KB entails notf.
1. Exemple d’utilisation
Tell operation
Tell: It is raining.
|
Possible responses: _ Already knew that: entailment (KB j= f) _ Don't believe that: contradiction (KB j= :f) _ Learned something new (update KB): contingent |
Ask operation
Ask: Is it raining?
|
Possible responses: _ Yes: entailment (KB j= f) _ No: contradiction (KB j= :f) _ I don't know: contingent |
Satisfiability
|
Definition: satisfiability A knowledge base KB is satisfiable if M(KB) != {}. |
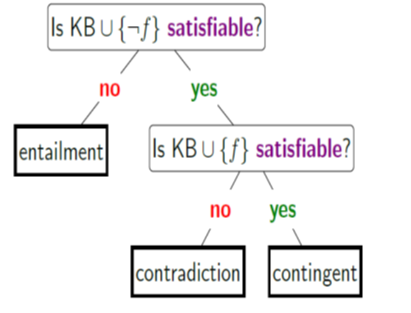
2. Reduce Ask[f] and Tell[f] to satisfiability
1. Model checking
|
Definition: model checking Input: knowledge base KB Output: exists satisfying model (M(KB) != {}) |
Checking satisfiability (SAT) in propositional logic is special case of solving CSPs!
2. Règles d’inférence
|
Key idea: inference rules Rules operate directly on syntax, not on semantics. |
Jusqu'ici, nous avons utilisé des formules, via la sémantique, pour définir des ensembles de modèles. Et tous nos raisonnements sur les formules sont basés sur ces modèles (par exemple, la réduction à la satisfaction). Les règles d'inférence nous permettent de raisonner sur les formules elles-mêmes sans jamais instancier les modèles.
Cela peut être assez puissant. Si vous avez une énorme base de connaissances avec beaucoup de formules et de symboles propositionnels, vous pouvez parfois tirer une conclusion sans instancier le problème de vérification de modèle complet. Ce sera très important lorsque nous passerons à la logique du premier ordre, où les modèles peuvent être infinis, et donc la vérification de modèle serait impossible.
3. Modus ponens
Capture le raisonnement de type if-then reasoning pattern.
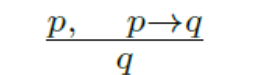

1. Algorithme d’Inférence


On ne peut pas dériver quelques formules
notWet, Rain =>Slippery
1. Soundness and completeness
The truth, the whole truth, and nothing but the truth.
_ Soundness: nothing but the truth
_ Completeness: whole truth
Modus ponens est Sound mais incomplet

1. Fixing completeness
|
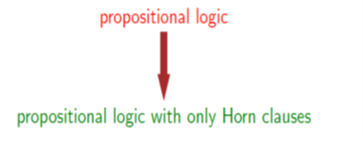
Option 1: Restrict the allowed set of formulas |
Option 2: Use more powerful inference rules |
 |
|
Definition: Definite clause
(p1 ^ ….^ pk) -> q / p1; … ; pk; q are propositional symbols.
Example: (Rain ^ Snow) -> Traffic
Example: Traffic
Non-example: notTrafficc
Non-example: (Rain ^ Snow) ->(Traffic ou Peaceful)
1. Horn clauses
Soit:
_ a definite clause (p1 ^…pk -> q)
_ a goal clause (p1 ^ … ^ pk -> false)
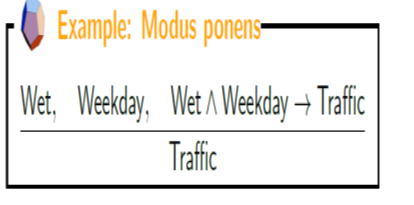
2. Modus ponens
generalized it to arbitrary number of premises
1. Completude
Theorem
Theorem: Modus ponens on Horn clauses
Modus ponens is complete with respect to Horn clauses:
_ Suppose KB contains only Horn clauses and p is an entailed propositional symbol.
_ Then applying modus ponens will derive p.
Exemple