3. Implementation de l’algorithme. 4
4. le pseudo code l’algorithme est. 4
5. La simulation de l’algorithme sur un arbre donné. 5
1. Minimax
L`algorithme MINIMAX calcule une valeur et l’affecte à la racine. le joueur MAX fera le choix de son coup selon cette valeur. L’algorithme fonctionne selon la procédure suivante :
- développer l’arbre de jeu pour P niveaux
- explorer l’arbre de jeu niveau par niveau de bas en haut, en commençant par les nœuds terminaux et en montant jusqu`à la racine:
- si le nœud courant p représente une position terminale, on lui affecte la valeur de la fonction d’évaluation statique, f(p).
- s'il s'agit d'une position intermédiaire et d'un nœud MIN on lui associe la plus petite des valeurs associées à ses fils
- s'il s'agit d'une position intermédiaire et d'un nœud MAX on lui associe la valeur maximale qui a été associée à ses fils
Quand on associe une valeur à la racine (appelée valeur MiniMax) selon cette procédure, le coup choisi sera le coup qui mène vers le fils qui a cette valeur maximale. En cas ou plusieurs fils ont cette valeur on fait un choix aléatoire ou on choisit le coup qui nous fait gagner quelques choses en plus selon certains critères(exemple : temps).
Un exemple est donné par la figure suivante .
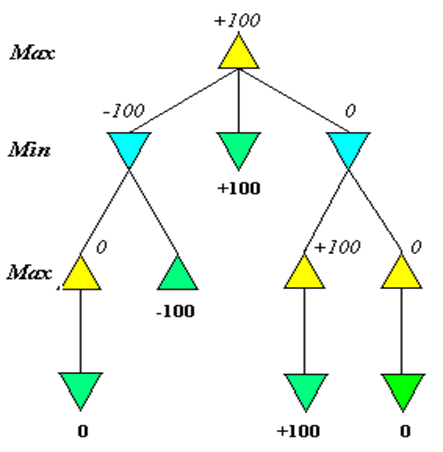
Figure 1. application de minimax.
L`algorithme MINIMAX est
Complet – oui si l`arbre de jeu est fini
Optimal – oui si le joueur MAX a un adversaire qui joue de façon
optimale
Complexité en temps - O(bP )
Complexité en espace – pour une exploration de l`arbre de jeu en profondeur d`abord O(bP)
Exemple de complexité en temps : le jeu d`échec a un facteur de branchement b=35 et pour des jeux communs P=100, donc on obtient un nombre de traitements de l`ordre 35100, ce qui est un nombre géant (pour faire une comparaison, le nombre des atomes de l`univers est de l'ordre de 10100. Il est nécessaire des trouver des stratégies plus pratiques.
2. L`élagage Alpha-Beta
L’algorithme minimax explore la totalité de l’arbre pour calculer la valeur de jeu. Mais dans certaines situations il n’est pas nécessaire d’examiner tous les nœuds. Par exemple dans l’arbre présenté par la figure 2. Carrée est max et cercle est un min.
Ici on se place a la place de la machine et on est maximiser. Et on veut savoir quel est le meilleur coup à faire pour gagner le maximum possible.
Coupure Alpha : (figure 2)
U a trouvé un coup qui lui a permet de gagner 5 (coup à gauche). Si on continue l’exploration en visitant le frère à droite V. v est minimiser et le premier coup à partir de cette position (coup à gauche ) lui permet de gagner 4 et puisque v est minimiser, et il est rationnel, son gain à partir de cette position sera au maximum 4 càd que v ne laissera jamais maximiser (u) gagnera plus que 4. Donc pour U il est inutile de continuer l’exploration de ce sous arbre parce qu’il n’aura pas plus que 4 et il a déjà un coup qui lui permet de gagner au moins cette valeur (ici 5 qui vient du coup à gauche).
Coupure Bêta : (figure 2)
Le même raisonnement est applicable à la situation à droite présenté par la figure 2.
le premier enfant du nœud Max V vaut 4 donc V vaudra au minimum 4. Le nœud Min U prendra donc la valeur 3 (minimum entre 3 et une valeur supérieure ou égale à 4).
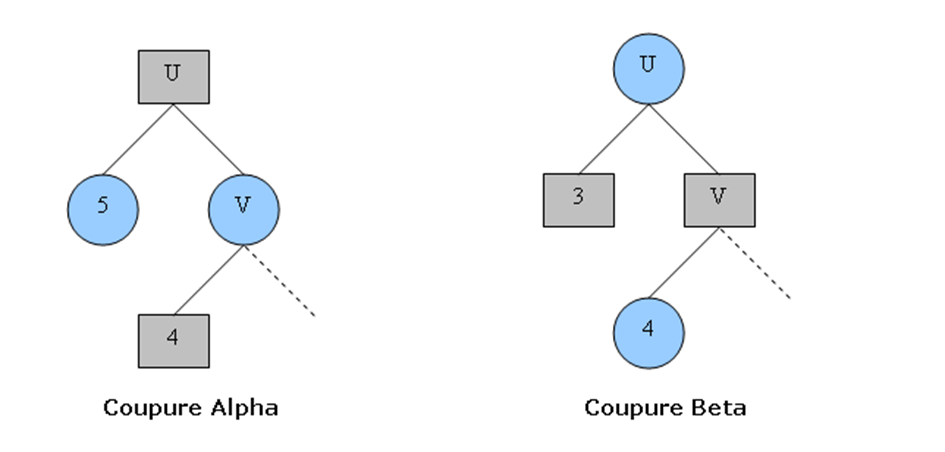
Figure 2 coupure alpha et beta.
L'élagage alpha-beta permet d’améliorer les performance (temps et mémoire) de minimax sans en modifier le résultat final.
Pour y faire, il n’explore que partiellement l’arbre de jeu. L’exploration partielle est la conséquence du fait suivant : il est inutile d'examiner les sous-arbres qui n’améliore pas la valeur de jeu déjà trouvé. Càd, si un coup est jugé mauvais par rapport à un autre déjà examiné, alors il est inutile (sans intérêt) d’examiner les conséquences de ce coup.
3. Implementation de l’algorithme
1. L’arbre de jeu est exploré selon l’approche DFS (depth first search). Une valeur est stockée à chaque nœud de l’arbre. Pour le cas du nœud max la valeur est appelée alpha. Et pour min, elle est appelée beta.
2. Une valeur alpha (α ) est la valeur maximale trouvée jusqu’à présent parmi toutes les valeurs des nœuds descendants de type max.
3. Une valeur Beta (β ) est la valeur minimale trouvée jusqu’à présent parmi toutes les valeurs des nœuds descendants de type min.
4. Et pour éviter la recherche des valeurs des ancêtres, ces valeurs sont transmises de haut en bas comme suit :
5. Pour chaque nœud max , le minimum parmi tous les ancêtres de type min est stocké comme beta.
6. Pour chaque nœud min , le maximum parmi tous les ancêtres de type max est stocké comme alpha.
Alors chaque nœud stocke une valeur alpha et beta.
7. A l’etat initial la valeur alpha du nœud racine est affecté la valeur moins l’infini(-∞) et beta= +∞
8. on arrête l’exploration dés que alpha>=beta.( α>= β)
4. le pseudo code l’algorithme est
Function alpha_beta (current_node, alpha, beta)
{
if is_root_node (current_node)
then
{
alpha = -infinity
beta = infinity
}
if is_leaf (current_node)
then return static_evaluation (current_node);
if is_max_node (current_node)
then
{
alpha = max (alpha, alpha_beta (children, alpha, beta));
if alpha >= beta
then cut_off_search_below (current_node);
}
if is_min_node (current_node)
then
{
beta = min (beta, alpha_beta (children, alpha, beta));
if beta <= alpha
then cut_off_search_below (current_node);
}
}
Pour voir comment il fonctionne en pratique, considrer l’arbre suivant
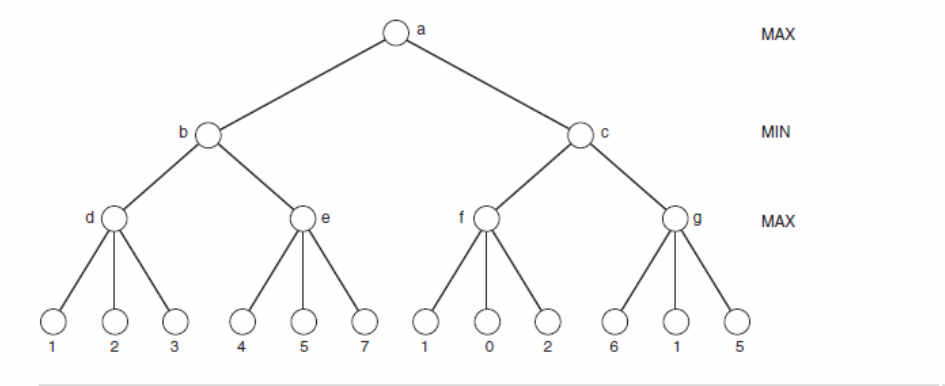
5. La simulation de l’algorithme sur un arbre donné
Au niveau des nœuds de type max on change alpha.
Et de type min on change beta. Cela est indiqué sur la figure en utilisant une police de grande taille et gras.
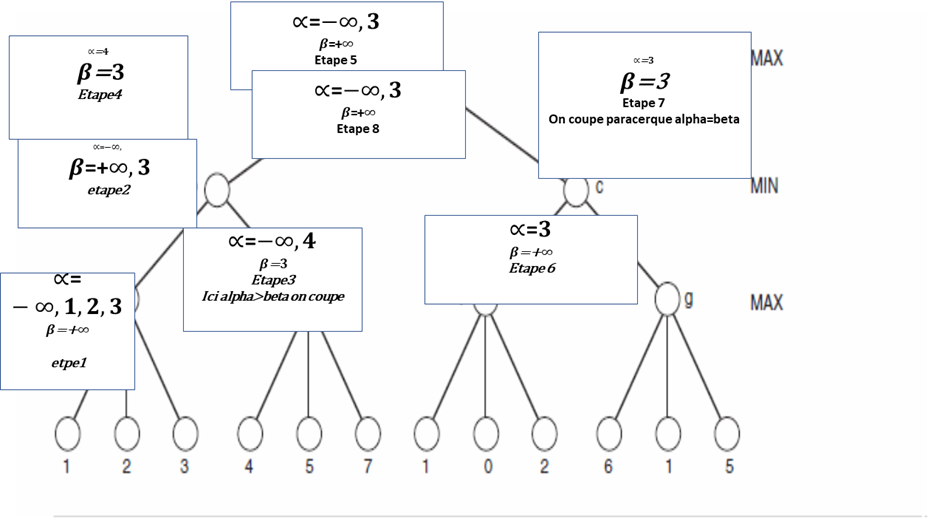
Les sous arbre élagués sont présentés sur la figure par un segment Blue.
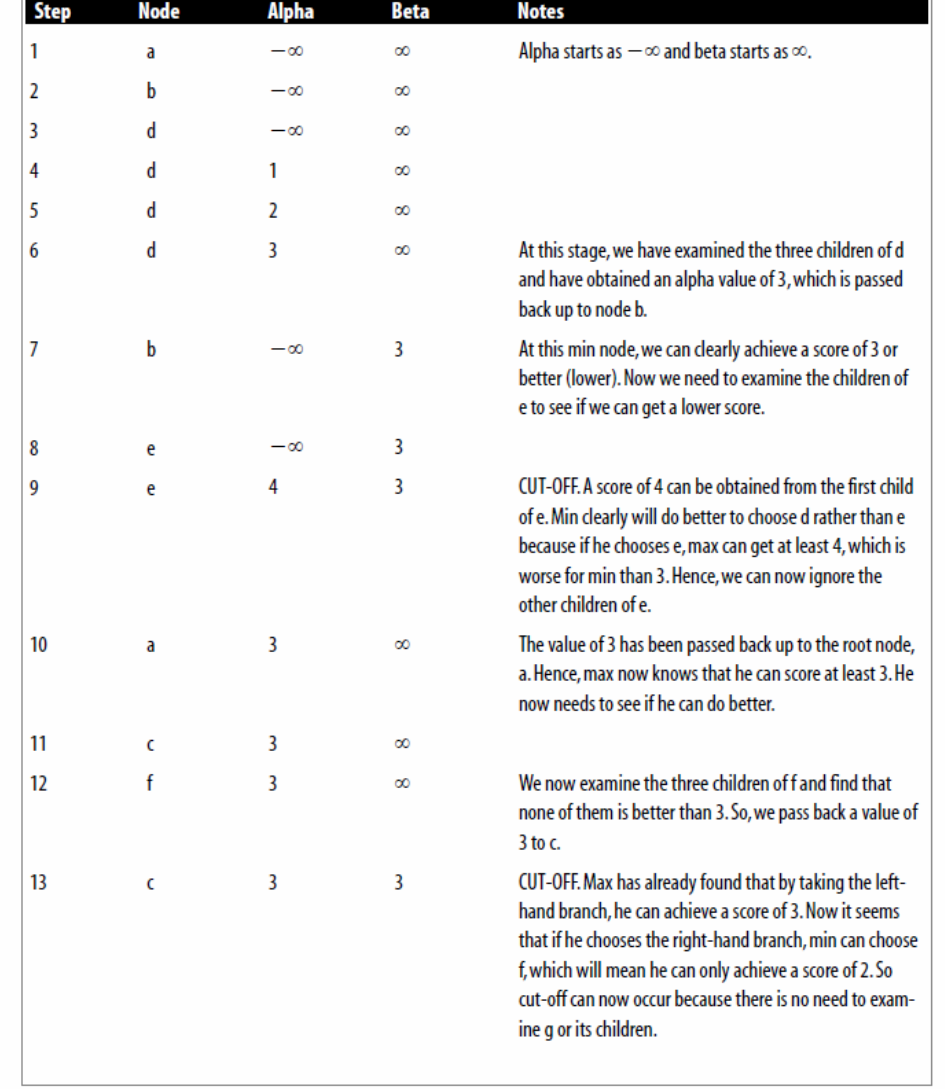
Une simulation tabulaire donne( le parcours utilise l’algorithme DFS)
6. Pour plus de détails
Livre Artificial intelligence : a modern appraoch de stuartj Russel et al.
Livre Artificial intelligence illuminated de ben coppin
http://turing.cs.pub.ro/auf2/html/chapters/
