1. Pourquoi l'analyse des performances ?

De nombreuses choses importantes doivent être prises en compte, comme la convivialité, la modularité, la sécurité, la maintenabilité, etc. Pourquoi se soucier des performances ?
La réponse à cette question est simple, nous ne pouvons avoir toutes les choses ci-dessus que si nous avons des performances. La performance est donc comme une monnaie grâce à laquelle nous pouvons acheter toutes les choses ci-dessus. Pour résumer, performance == échelle. Imaginez un éditeur de texte qui peut charger 1000 pages, mais peut vérifier l'orthographe 1 page par minute OU un éditeur d'image qui prend 1 heure pour faire pivoter votre image de 90 degrés vers la gauche OU… vous l'avez compris. Si une fonctionnalité logicielle ne peut pas faire face à l'ampleur des tâches que les utilisateurs doivent effectuer, elle est pratiquement morte.

1.1. Étant donné deux algorithmes pour une tâche, comment savoir lequel est le meilleur ?
Une façon naïve de le faire est d'implémenter les deux algorithmes et d'exécuter les deux programmes sur votre ordinateur pour différentes entrées et de voir lequel prend le moins de temps. Il y a beaucoup de problèmes avec cette approche pour l'analyse des algorithmes.
1) Il est possible que pour certaines entrées, le premier algorithme fonctionne mieux que le second. Et pour certaines entrées, la seconde fonctionne mieux.
2) Il est également possible que pour certaines entrées, le premier algorithme fonctionne mieux sur une machine et que le second fonctionne mieux sur une autre machine pour certaines autres entrées.

1.2. L'analyse asymptotique 

est la grande idée qui gère les problèmes ci-dessus dans l'analyse des algorithmes. Dans l'analyse asymptotique, nous évaluons les performances d'un algorithme en termes de taille d'entrée (nous ne mesurons pas le temps d'exécution réel). Nous calculons comment le temps (ou l'espace) pris par un algorithme augmente avec la taille de l'entrée.
Par exemple, considérons le problème de recherche (recherche d'un élément donné) dans un tableau trié. Une méthode de recherche est la recherche linéaire (l'ordre de croissance est linéaire) et l'autre méthode est la recherche binaire (l'ordre de croissance est logarithmique). Pour comprendre comment l'analyse asymptotique résout les problèmes mentionnés ci-dessus dans l'analyse des algorithmes, disons que nous exécutons la recherche linéaire sur un ordinateur rapide A et la recherche binaire sur un ordinateur lent Bet nous choisissons les valeurs constantes pour les deux ordinateurs afin qu'elles nous indiquent exactement combien de temps il faut à la machine donnée pour effectuer la recherche en secondes. Disons que la constante pour A est 0,2 et la constante pour B est 1000, ce qui signifie que A est 5000 fois plus puissant que B. Pour de petites valeurs de taille de tableau d'entrée n, l'ordinateur rapide peut prendre moins de temps. Mais, après une certaine valeur de taille de tableau d'entrée, la recherche binaire commencera certainement à prendre moins de temps par rapport à la recherche linéaire, même si la recherche binaire est exécutée sur une machine lente. La raison en est que l'ordre de croissance de la recherche binaire par rapport à la taille de l'entrée est logarithmique, tandis que l'ordre de croissance de la recherche linéaire est linéaire. Ainsi, les constantes dépendantes de la machine peuvent toujours être ignorées après une certaine valeur de taille d'entrée.
Voici quelques temps d'exécution pour cet exemple :
Temps d'exécution de la recherche linéaire en secondes sur A : 0,2 * n
Temps d'exécution de la recherche binaire en secondes sur B : 1000*log

1.3. L'analyse asymptotique fonctionne-t-elle toujours ?
L'analyse asymptotique n'est pas parfaite, mais c'est le meilleur moyen disponible pour analyser les algorithmes. Par exemple, disons qu'il y a deux algorithmes de tri qui prennent respectivement 1000nLogn et 2nLogn sur une machine. Ces deux algorithmes sont asymptotiquement identiques (l'ordre de croissance est nLogn). Ainsi, avec l'analyse asymptotique, nous ne pouvons pas juger lequel est le meilleur car nous ignorons les constantes de l'analyse asymptotique.
De plus, dans l'analyse asymptotique, nous parlons toujours de tailles d'entrée supérieures à une valeur constante. Il est possible que ces entrées importantes ne soient jamais transmises à votre logiciel et qu'un algorithme asymptotiquement plus lent fonctionne toujours mieux dans votre situation particulière. Ainsi, vous pouvez finir par choisir un algorithme asymptotiquement plus lent mais plus rapide pour votre logiciel.

1.4. Notations de landau :

Il existe principalement 3 notations de complexité temporelle :

1.4.1. Notation Big O

Nous définissons la complexité temporelle d'un algorithme dans le pire des cas en utilisant la notation Big-O, qui détermine que l'ensemble de fonctions croît plus lentement ou au même rythme que l'expression. De plus, il explique le temps maximum nécessaire à un algorithme pour prendre en compte toutes les valeurs d'entrée.

1.4.2. Notation Oméga

Elle définit le meilleur cas de la complexité temporelle d'un algorithme, la notation Omega définit si l'ensemble de fonctions va croître plus vite ou au même rythme que l'expression. En outre, il explique le temps minimum requis par un algorithme pour prendre en compte toutes les valeurs d'entrée.

1.4.3. Notation thêta

Il définit le cas moyen de la complexité temporelle d'un algorithme, la notation Thêta définit quand l'ensemble de fonctions se situe à la fois dans O(expression) et Omega(expression) , puis la notation Thêta est utilisée. C'est ainsi que nous définissons un cas moyen de complexité temporelle pour un algorithme. 

1.5. Mesure de la complexité d'un algorithme

Sur la base des trois notations de complexité temporelle ci-dessus, il existe trois cas pour analyser un algorithme :

1.5.1. Analyse du pire cas (principalement utilisée) 

Dans l'analyse du pire des cas, nous calculons la borne supérieure du temps d'exécution d'un algorithme. Il faut connaître le cas qui provoque l'exécution d'un nombre maximum d'opérations. Pour la recherche linéaire, le pire des cas se produit lorsque l'élément à rechercher ( x dans le code ci-dessus) n'est pas présent dans le tableau. Lorsque x n'est pas présent, la fonction search() le compare avec tous les éléments de arr[] un par un. Par conséquent, la complexité temporelle dans le pire des cas de la recherche linéaire serait Θ .

1.5.2. Analyse du meilleur cas (très rarement utilisé) 

Dans le meilleur des cas, nous calculons la borne inférieure sur le temps d'exécution d'un algorithme. Il faut connaître le cas qui provoque l'exécution d'un nombre minimum d'opérations. Dans le problème de recherche linéaire, le meilleur cas se produit lorsque x est présent au premier emplacement. Le nombre d'opérations dans le meilleur des cas est constant (indépendant de n). Donc la complexité temporelle dans le meilleur des cas serait Θ(1) 

1.5.3. Analyse de cas moyenne (rarement utilisée) 

Dans une analyse de cas moyenne, nous prenons toutes les entrées possibles et calculons le temps de calcul pour toutes les entrées. Additionnez toutes les valeurs calculées et divisez la somme par le nombre total d'entrées. Il faut connaître (ou prédire) la distribution des cas. Pour le problème de recherche linéaire, supposons que tous les cas sont uniformément distribués (y compris le cas où x n'est pas présent dans le tableau). Nous additionnons donc tous les cas et divisons la somme par (n+1). Voici la valeur de la complexité temporelle moyenne des cas.

Temps de cas moyen = \sum_{i=1}^{n}\frac{\theta (i)}{(n+1)} = \frac{\theta (\frac{(n+1)*(n+ 2)}{2})}{(n+1)} = \thêta

1.5.4. Quelle analyse de complexité est généralement utilisée ?

Vous trouverez ci-dessous la mention classée de la notation d'analyse de complexité en fonction de la popularité :

1.5.6. Analyse du pire cas : 

La plupart du temps, nous effectuons des analyses du pire des cas pour analyser les algorithmes. Dans la pire analyse, nous garantissons une borne supérieure sur le temps d'exécution d'un algorithme qui est une bonne information. 

1.5.7. Analyse de cas moyenne 

L'analyse de cas moyenne n'est pas facile à faire dans la plupart des cas pratiques et elle est rarement effectuée. Dans l'analyse du cas moyen, nous devons connaître (ou prédire) la distribution mathématique de toutes les entrées possibles. 

1.5.8. Analyse du meilleur cas 

L'analyse du meilleur cas est fausse. Garantir une borne inférieure sur un algorithme ne fournit aucune information car dans le pire des cas, un algorithme peut prendre des années à s'exécuter.

1.6 notations petit o et petit oméga

L'idée principale de l'analyse asymptotique est d'avoir une mesure de l'efficacité des algorithmes qui ne dépendent pas de constantes spécifiques à la machine, principalement parce que cette analyse ne nécessite pas la mise en œuvre d'algorithmes et le temps pris par les programmes pour être comparés. Nous avons déjà discuté précédement les trois principales notations asymptotiques. Les 2 notations plus asymptotiques suivantes sont utilisées pour représenter la complexité temporelle des algorithmes

Petite notation ο asymptotique

Big-Ο est utilisé comme une borne supérieure étroite sur la croissance de l'effort d'un algorithme (cet effort est décrit par la fonction f), même si, tel qu'il est écrit, il peut également s'agir d'une borne supérieure lâche. La notation "petit-ο" (ο()) est utilisée pour décrire une borne supérieure qui ne peut pas être serrée. 

Définition : Soit f et g des fonctions qui associent des entiers positifs à des nombres réels positifs. On dit que f vaut ο(g) (ou f Ε ο(g)) si pour toute constante réelle c > 0, il existe une constante entière n0 ≥ 1 telle que 0 ≤ f <c*g.

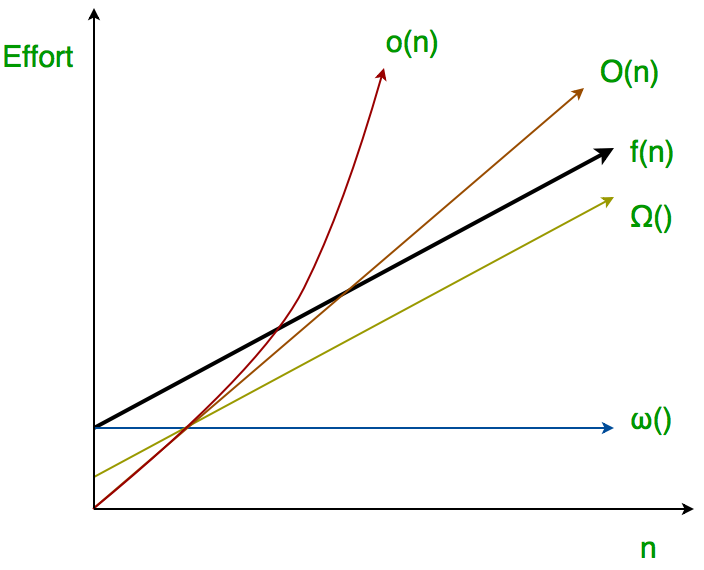
 Ainsi, petit o() signifie une limite supérieure lâche de f. Little o est une estimation approximative de l'ordre maximum de croissance alors que Big-Ο peut être l'ordre réel de croissance. 
En relation mathématique, f = o(g) signifie lim f/g = 0 n→∞ 

Exempl

Ainsi, petit o() signifie une limite supérieure lâche de f. Little o est une estimation approximative de l'ordre maximum de croissance alors que Big-Ο peut être l'ordre réel de croissance. 
En relation mathématique, f = o(g) signifie lim f/g = 0 n→∞ 

Exemples:

Est-ce que 7n + 8 ∈ o(n 2 ) ? 

Pour que cela soit vrai, pour tout c, il faut pouvoir trouver un n0 qui fasse 

f < c * g asymptotiquement vrai. 

Prenons un exemple, 

Si c = 100, on vérifie que l'inégalité est clairement vraie. Si c = 1/100 , nous devrons utiliser 

un peu plus d'imagination, mais on pourra trouver un n0. (Essayez n0 = 1000.) De 

ces exemples, la conjecture semble correcte. 

puis vérifier les limites, 

lim f/g = lim (7n + 8)/(n 2 ) = lim 7/2n = 0 (l'hôpital) 

n→∞ n→∞ n→∞ 

donc 7n + 8 ∈ o(n 2 )

Little ω asymptotic notation

Définition : Soient f et g des fonctions qui associent des entiers positifs à des nombres réels positifs. On dit que f est ω(g) (ou f ∈ ω(g)) si pour toute constante réelle c > 0, il existe une constante entière n0 ≥ 1 telle que f > c * g ≥ 0 pour tout entier n ≥ n0. 

f a un taux de croissance plus élevé que g donc la principale différence entre Big Omega (Ω) et little omega (ω) réside dans leurs définitions. Dans le cas de Big Omega f=Ω(g(n )) et la borne est 0<=cg<=f, mais en cas de petit oméga, c'est vrai pour 0<=c*g<f. 

La relation entre Big Omega (Ω) et Little Omega (ω) est similaire à celle de Big-Ο et Little o sauf que nous examinons maintenant les bornes inférieures. Little Omega (ω) est une estimation approximative de l'ordre de croissance alors que Big Omega (Ω) peut représenter l'ordre exact de croissance. Nous utilisons la notation ω pour dénoter une borne inférieure qui n'est pas asymptotiquement étroite. Et, f ∈ ω(g) si et seulement si g ∈ ο((f). 

En relation mathématique, 

si f ∈ ω(g) alors, 

lim f/g = ∞ 

n→∞ 

Exemple: 

Montrer que 4n + 6 ∈ ω(1); 

le temps de fonctionnement du petit oméga (ο) peut être prouvé en appliquant la formule limite donnée ci-dessous. 

si lim f/g = ∞ alors les fonctions f est ω(g) 

n→∞ 

ici, on a les fonctions f=4n+6 et g=1 

lim (4n+6)/(1) = ∞ 

n→∞ 

et aussi pour tout c nous pouvons obtenir n0 pour cette inégalité 0 <= c*g < f, 0 <= c*1 < 4n+6 

Donc prouvé.