Minimisation de l’erreur de prédiction
On a vu que les paramètres d’un modèle sont identifiés en minimisant un critère quadratiques basé sur l’erreur de prédiction définie comme :
Pour les structures FIR et ARX, l’erreur de
prédiction est linéaire par rapport au vecteur de paramètres à identifier et donc le minimum du critère peut être calculé avec
la méthode des moindres carrés. Les autres structures résultent en un problème
d’optimisation non linéaire pour laquelle on
utilise
le plus souvent l’algorithme itératif de Gauss-Newton.
Méthode de Gauss-Newton(méthode de gradient)
Dans de nombreuses applications , la fonction modèle n’est pas linéaire par rapport à ses paramètres
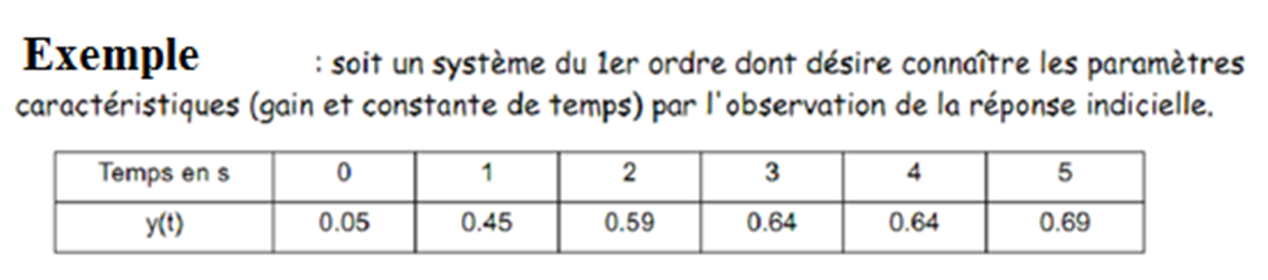
Exemple : réponse indicielle d’un circuit du 1erordre
L’expression du modèle est :
Avec
La dépendance vis-à-vis du paramètre est non-linéaire, il n’est plus possible de
résoudre le système par la méthode linéaire (pas de matrice H)
La proposition est a partir d’une valeur
initiale des
paramètres et de modifier itérativement la valeur de
d’un
incrément
de
façon à minimiser le critère d’erreur quadratique cumulée
a chaque
étape.
Etape initiale
Pour
Le modèle prend les valeurs :
L’erreur entre modèle et
les mesures est :
L’erreur quadratique cumulée est :
Généralement, l’erreur cumulée sera importante, les conditions initiales étant éloignées de la solution optimale.
Incrémentation
Modification de la valeurPour se placer au minimum d’erreur, on choisit
Calcule du minimum de l’erreur cumulée
Calcule
de 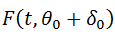 par le
développement de Taylor du 1er ordre du modèle qui permet d’approximer la nouvelle valeur du
modèle à chaque instant d’observation :
par le
développement de Taylor du 1er ordre du modèle qui permet d’approximer la nouvelle valeur du
modèle à chaque instant d’observation :
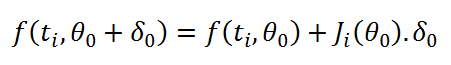
Avec 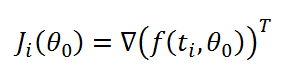 gradient de f en ligne
gradient de f en ligne
L’extension à l’ensemble des points de calcules prend la forme matricielle suivantes :
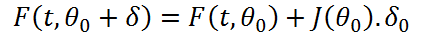
Avec
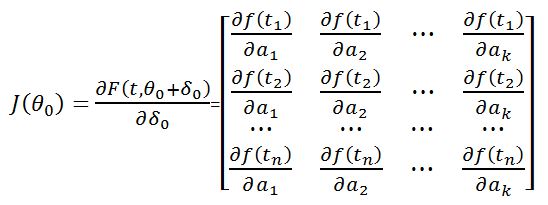
jacobienne de f/ paramètres
Calcul du minimum de l’erreur cumulée :
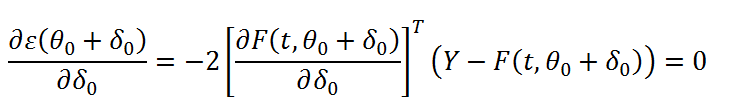
D’où 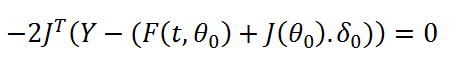
On en déduit la valeur de l’accroissement à faire
sur les paramètres pour minimiser l’erreur :
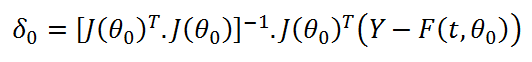
Itération
On itère en définissant les nouvelles valeurs
des paramètres 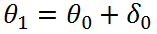 et les nouvelles valeurs
du modèle
et les nouvelles valeurs
du modèle 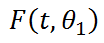 . la correction suivantes à faire sera :
. la correction suivantes à faire sera :
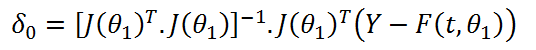
Remarque : certaines valeurs initiales ne permettent pas à l’algorithme de converger
L’inversion de la matrice 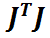 peut poser
problème (matrice singulière) . pour
éviter se blocage on propose l’algorithme suivante de (Levenberg-
Marquardt ) suivantes :
peut poser
problème (matrice singulière) . pour
éviter se blocage on propose l’algorithme suivante de (Levenberg-
Marquardt ) suivantes :
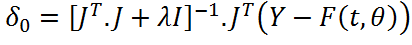
Le paramètres \( \lambda \) joue le rôle d’un amortissement de la
correction ; il doit être ajusté à chaque pas de calcul. Dans le cas
simples on peut se contenter
d’un amortissement constant, dont la valeur initiale a été proposée par Marquardt :
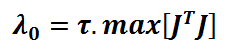
\( \tau \) est un paramètre de gain a choisir convenablement.