Recherche dans les arbres de jeux
7. Recherche dans les arbres de jeux. 5
1. But de cours
Dans ce cours, on va étudier les arbres de jeux, et on va voir comment modéliser différents
situations de jeu en utilisant les arbres de jeu. Nous étudierons aussi les algorithmes classiques
de recherche dans les arbres de jeu (MINIMAX et l’élagage alpha-beta ) et comment savoir quand on est dans une meilleure position ou dans une mauvaise situation.
2. Introduction
Le jeu est une activité qui requiert de l’intelligence. Les jeux de société placent les joueurs dans des situations compétitives où chacun, à tour de rôle, doit prendre une d´décision sans connaître celle que prendra ensuite l’adversaire. Les êtres humains, pour résoudre ce problème, raisonnent classiquement en développant `a l’avance un certain nombre de coups aussi bien amis qu’ennemis : si je joue un tel coup, alors l’adversaire peut répondre tel ou tel autre coup ; après l’un de ceux-ci, j’ai telle et telle riposte `a ma disposition et ainsi de suite. Une arborescence des coups l´égaux, et donc des situations possibles, est ainsi engendrée(figure 1) , où les coups amis et ennemis alternent `a chaque changement de niveau.
Après un certain temps de réflexion, le joueur humain, pesant le pour et le contre des différentes situations, se décide pour le coup du premier niveau qu’il juge le meilleur et il le joue. Les programmes de jeux sur ordinateurs ne procèdent pas autrement. ce document présente la façon dont un tel programme construit son arborescence de recherche et l’intérêt de cette dernière. Ensuite, il présente la manière de juger de la valeur des positions obtenues. Ceci se fait à l’aide de ce qu’on appelle depuis 1950, avec Claude Shannon. une fonction d´évaluation. Enfin, il présente les méthodes pour choisir le coup à jouer après ces développements.
Nous considérons des jeux à deux joueurs avec information parfaite, i.e. chaque joueur est au courant de ce que l’autre joueur a fait ou peut en faire et à somme nul ( les gains de l’un sont les pertes de l’autre).
Cette famille est une famille dans laquelle se trouvent la plupart des jeux de réflexion (Othello, évidemment, mais aussi échecs, morpion, puissance 4, Go, etc).
somme nulle : les gains d’un joueur sont exactement l’opposé des gains de l’autre joueur (ces gains peuvent donc être négatifs) ;
information complète : lors de sa prise de décision (i.e. du choix d’un coup à jouer dans le cas qui nous intéresse), chaque joueur connaît précisément
– ses possibilités d’action ;
– les possibilités d’action de son opposant (c’est-à-dire les répliques possibles de l’adversaire dans le cas d’Othello) ;
– les gains résultants de ces actions.
Le joueur qui commence s’appelle le joueur MAX ( ) et l’autre joueur s’appelle MIN ( ). Ceci parce que – celui qui commence cherche à trouver, parmi toutes les situations qui est a sa disposition, une situation qui lui permet de maximiser ses gains ; – celui qui répond doit trouver, à partir de toutes les situations qui conduisent à la victoire du premier joueur, la situation qui minimise les gains de ce joueur.
3. Théorème du Minimax .
Théorème . . Pour tout jeu à deux joueurs, à somme nulle, avec un nombre fini de stratégies, il existe une valeur V et une stratégie mixte pour chaque joueur telle que (a) étant donnée la stratégie du joueur 2, le meilleur gain possible pour le joueur A est V, et (b) étant donnée la stratégie du joueur B, le meilleur gain possible pour le joueur est −V
4. Quelques définitions . .
▸ Le joueur A est appelé le joueur maximisant (ou joueur),
le joueur B est appelé le joueur minimisant (ou adversaire)
▸ par ex : la machine est le joueur maximisant.
▸ On appelle état du jeu une configuration du jeu
▸ par ex : l’état d’un jeu d’échec est l’enregistrement de toutes les positions des pièces sur l’échiquier
▸ On appelle état initial l’état de jeu avant que les joueurs aient joué, et état final un état mettant fin au jeu (gagné, perdu, égalité)
▸ On appelle gain d’un état la valeur gagnée par un joueur s’il atteint l’état donné
▸ On appelle coup une action permettant de passer le jeu d’un état à un autre ▸ par ex : déplacer un pion de X en Y
▸ On appelle fils d’un état ei , notés f(ei) les états atteignables depuis l’état ei → exploration d’un arbre de jeu
5. Motivation
Je vais commencer par vous montrer comment on va représenter un jeu par un arbre dite arbre de jeu.
Le jeu considéré ici et le tictactoe. Le tic-tac-toe, aussi appelé « morpion » (par analogie au jeu de morpion) et « oxo » en Belgique, est un jeu de réflexion se pratiquant à deux joueurs au tour par tour dont le but est de créer le premier un alignement. Le jeu se joue généralement avec papier et crayon (Wikipedia). Un joueur met des circle(o) et l’autre des croix (x).
Supposons que le premier met des croix alors il a 9 actions (coups ou choix)possibles (voir figure 1).
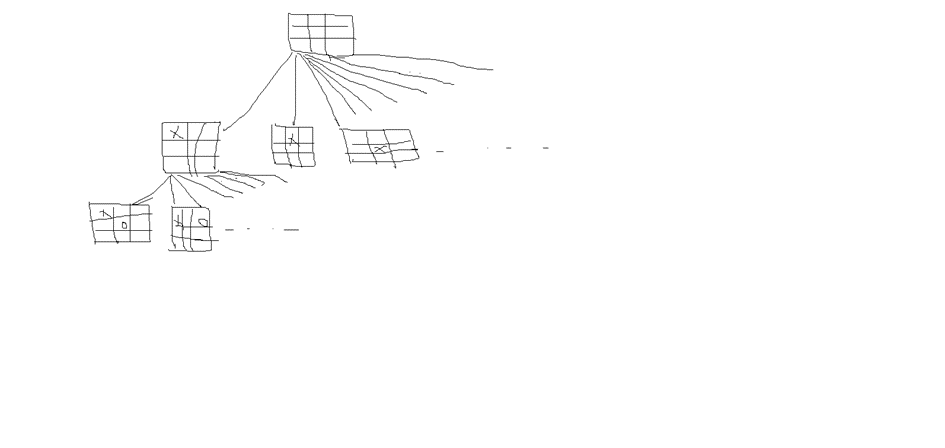
Figure 1. représentation partielle du jeu tictactoe
Puis Le deuxième joueur à 8 choix (actions ou coups) et ainsi de suite. Le jeu continue jusqu’à un des joueur gagne ou on arrive à une partie null.
On peut voir que ce jeu peut être représenté par un arbre.
Plusieurs jeux à deux joueurs peuvent être représentés par un arbre dite arbre de jeu.
La racine de l’arbre est la configuration initiale de jeu (situation de jeu avant toute action possible).
Les nœuds sont les configuration possible de jeu.
Les arcs : les actions (coups) possibles.
Les coups des deux joueurs sont représentés par des niveaux qui alternent. Càd que tous les arcs qui mènent du racine au premier niveau représente les coups du premier joueur nommé maximiser(MAX) et représenté par le triangle
Les arcs qui lient le premier nivaux avec le deuxième niveaux représentent les coups (move) des 2 joueur et ainsi de suite.
Les feuilles de l’arbre représente les états finaux de jeu (gagné, perdu, égalité) .
Dans les jeux simple un état final représente l’état ou la machine à gagné, perdue ou partie nul.
Mais dans les jeux complexe tel que GO, chess ..etc. le concept de l’état final est rarement utilisé.
Une approche pour programmer la machine pour qu’elle joue et gagne pourrait être l’utilisation d’un algorithme de recherche déjà vue aux cours précédents tels que, DFS, BFS( la recherche en profondeur d’abord ou en largeur d’abord) pour trouver un état final ou la machine gagne. Malheureusement cette approche n’est pas praticable parce qu’il y a un autre joueur intelligent (machine ou humain) et rational qui joue pour qu’il gagne.
Donc il faut chercher un autre algorithme pour que la machine puisse exploiter l’arbre de jeu pour prendre des décisions càd qu’elle sélectionne le meilleur coup ( le coup qu’il lui permettre de maximiser les gains ou de gagner) à chaque fois qu’il est son tour de jeu.
6. Fonction d’évaluation
Pour que la machine peut exploiter l’arbre de jeu pour jouer et gagner au jeu, elle a besoin d’une fonction d’évaluation f. cette fonction lui permettre de juger la qualité d’une configuration de jeu(combien la machine va gagner à partir de cette position). Parce que dans les jeux complexe tels que go et chess et vu le nombre assez large des configurations possibles de jeu , il n’est pas possible d’atteindre les états finaux( gagne, perdre, null).
Dans le cas du jeu de chess, une fonction d’évaluation f peut combiner des informations tels que le nombres de pièces restantes, la qualité de chaque pièce .. etc. pour produire une valeur représentant la qualité de la position.
7. Recherche dans les arbres de jeux
Même pour des arbres de jeux simples tel que l’arbre du tictactoe présenté partiellement par la figure 1. Il est impossible pour la machine de l’explorer totalement(exhaustivement) parce qu’il a une profondeur minimale de 9 et un facteur de branchement maximal de 9. Cela veut dire que la taille de l’espace d’états (arbre) est 9 != 350,000 états. Cette valeur peut être considéré comme petite mais pour des jeux tels que chess et go la taille sera très élevée. La machine généralement construit l’arbre jusqu’à un profondeur donnée et utilise une fonction d’évaluation pour évaluer les états de ce niveau.
8. MINIMAX
MinMax est un algorithme, et plus généralement une stratégie, qui provient du domaine de la « Théorie des jeux » et a été identifié par Von Neumann il y a plus de 60 ans.
Théorème du Minimax .
Théorème . . Pour tout jeu à deux joueurs, à somme nulle, avec un nombre fini de stratégies, il existe une valeur V et une stratégie mixte pour chaque joueur telle que (a) étant donnée la stratégie du joueur 2, le meilleur gain possible pour le joueur A est V, et (b) étant donnée la stratégie du joueur B, le meilleur gain possible pour le joueur est −V.
Nous considérons ici que la machine est un maximiser et l’opposant est un minimiser.
L’algorithme minimax est utilisé pour trouver le meilleur coup du jeu( le coup qui maximise le gain).
Le principe de la recherche d’un coup par MinMax est un processus base sur le même processus de réflexion que chacun de nous a déjà mis en œuvre. A partir d’une position donnée, on suppose que c’est au joueur max de jouer. Dans la position donnée, max a un certain nombre de coups q’il peut effectuer : pour chaque coup , il analyse les répliques éventuelles de l’adversaire min, qui lui-même analyse en utilisant le même principe. pour chacune de ses répliques celles auxquelles peut procéder max, qui à son tour examine à nouveau l’ensemble des coups qu’il peut effectuer suite aux répliques de min, etc. Ce processus de réflexion peut continuer ainsi et, dans le cas où les deux joueurs ont la capacité de mener cette réflexion jusqu’à ce qu’aucun des 2 joueurs ne puisse plus jouer alors il est facile pour max de décider du coup qu’il doit jouer. Il lui suffit en effet de choisir le coup qui, s’il existe, quelque soit la suite de répliques de max et min imaginées mène à une victoire.
La figure 2 montre comment fonctionne l’algorithme dans le cas d’un petit arbre.
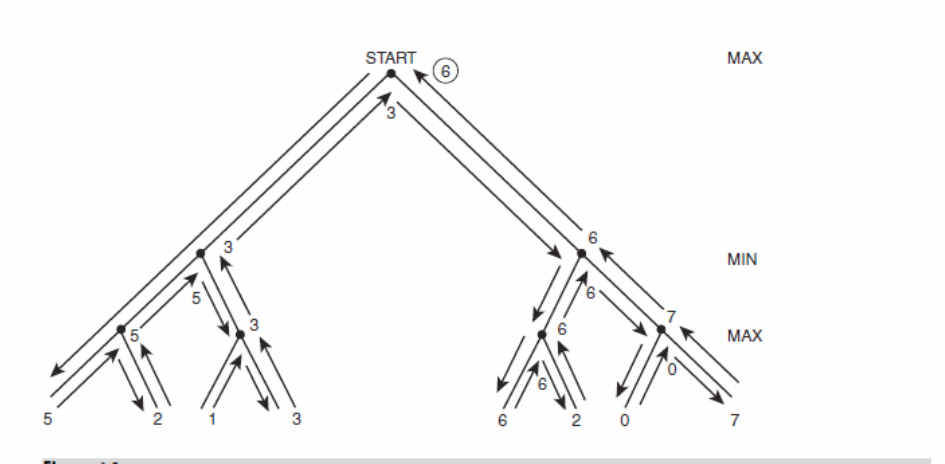
Figure 2. principe de fonctionnement de minimax
Noter que le meilleur gain que max peut l’avoir est 6.
si max choisit l’action ou le coup à gauche. alors min comme agent rationnel choisira le coup à droite laissant max avec les choix 1 et 3. Max est aussi rationnel est il cherche à maximiser le gain choisira 3. Si max commence son choix par le coup à droite min aura le choix entre 7 et 6. Alors il choisira le coup à gauche lassant max avec deux choix 2 et 6.
La figure montre aussi comment minimax utilise dfs (depth first search ) pour explorer l’arbre.
Le minimax calcul le meilleur coup à partir d’une position donnée par la fonction suivante :
Function minimax (current_node)
{ if is_leaf (current_node) then return static_evaluation (current_node);
if is_min_node (current_node) then return min (minimax (children_of (current_node)));
if is_max_node (current_node) then return max (minimax (children_of (current_node)));
// this point will never be reached since
// every node must be a leaf node, a min node or a
// max node. }
Un exemple est donné par la figure 3
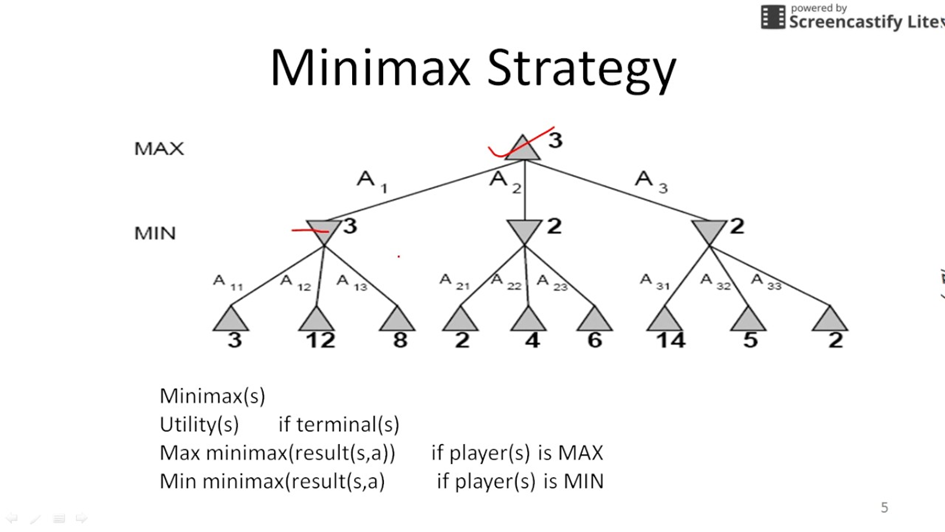
Figure 3. exemple de fonctionnement de minmax
9. Références
1. Artificial Intelligence illuminated Ben coppen.
2. Intelligence Artificielle Résolution de problèmes par l’Homme et la machine Jean-Louis Laurière.
Remarque
Merci de nous envoyer des suggestions pour améliorer la forme et le fond de ce document.
