Table des matières
1. Résolution de problème en IA.. 1
3. Techniques d’exploration. 3
5. Critères de comparaison des algorithmes de recherches. 3
6. Techniques d’exploration aveugles. 3
7. Comparaison des algorithmes. 4
États : la description d’un état spécifie l’emplacement des huit pièces et celui de la case vide.
• État initial : n’importe quel état peut être pris comme état initial.
• O : déplacement vers Gauche, Droite, Haut ou Bas.
. F : Test de l’état final : celui-ci vérifie si l’état correspond à la configuration finale
(D’autres configurations finales sont envisageables.)
• C : le coût de chaque étape est 1, le coût du chemin est égal au nombre d’étapes qui composent le chemin.
Exemple 2
L’objectif du problème des 8 reines est de placer huit reines sur un échiquier de façon à ce qu’aucune d’elles n’en menace une autre.
Formulation de problème
• États : toute disposition de O à 8 reines sur l’échiquier constitue un état.
• État initial: pas de reine sur l’échiquier.
• Fonction successeur : poser une reine sur l’une des cases vides. • Test de l’état final : huit reines sur l’échiquier et aucune menacée.
Selon cette formulation, on a 64 x
63 x... x 57 ![]() 1,8 x 1014
séquences possibles à examiner.
1,8 x 1014
séquences possibles à examiner.

Figure : une mauvaise solution
3. Techniques d’exploration
4. Algorithme de base :
1. Initialisation : Set Open ={E0}
2. Fail if open ={} terminer avec échec
3. Sélectionner un état n de open
4. Terminer : si n est but alors terminer avec succès
5. Etendre : générer le successeurs de n en utilisant O et placez-les dans open.
6. Loop : Aller à 2
5. Critères de comparaison des algorithmes de recherches
Complétude : a-t-on une garantie de trouver une solution quand elle existe ?
Complexité du temps de calcul : combien de temps a-t-on besoin (dans le pire des cas)
Complexité de l’espace mémoire : combien d’espace mémoire a-t-on besoin (dans le pire des cas)
Optimalité : est-ce-que la solution trouvée est optimale ?
6. Techniques d’exploration aveugles
· expansion d’un graphe en largeur d’abord(“breadth-first search” (BFS))
· expansion d’un graphe en profondeur d’abord (“depth-first search” (DFS))
· expansion d’un graphe avec côut uniforme (“Uniform-cost search”) : développer le noeud qui a le coût le plus bas.
· recherche en profondeur limitée (“depth-limited search”) : utilise DFS jusqu’à une profondeur l donnée cela évite le problème du chemin infini, mais pause problème si la solution est plus profonde que l.
· recherche en profondeur itérative (“iterative deepening DFS”) : combine DFS et BFS : itérativement utilise DFS jusqu’à une profondeur de 1, 2, ... jusqu’à trouver le but. les états sont générés de nombreuses fois
· recherche bidirectionnelle (“Bidirectional search”) : effectue deux recherche : une de l’état initial vers l’état final, l’autre dans le sens inverse (donc depuis l’état final).
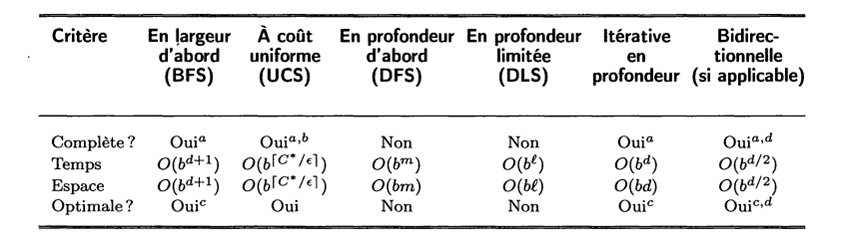
7. Comparaison des algorithmes
b sera le facteur de branchement de l’arbre
d est la profondeur de la solution la moins profonde
m est la profondeur maximale de l’arbre de recherche
l est la limite de profondeur