1 Introduction

L’identification consiste a déterminer les paramètres d’un modèle mathématique, dont la structure est établie selon un critère donné , les paramètres des modèles sont obtenus par la minimisation de l’erreur de prédiction entre le signal de sortie mesuré et le signal estimé suivant un critère d’optimalité par exemple : (moindres carrés, erreur quadratique moyenne, maximum de vraisemblance), nous nous intéressons plus particulièrement à la méthode qui est basée sur le blanchissement de l’erreur de prédiction . Formellement l’opération d’identification des paramètres du modèle peut se résumer par la figure ci-dessous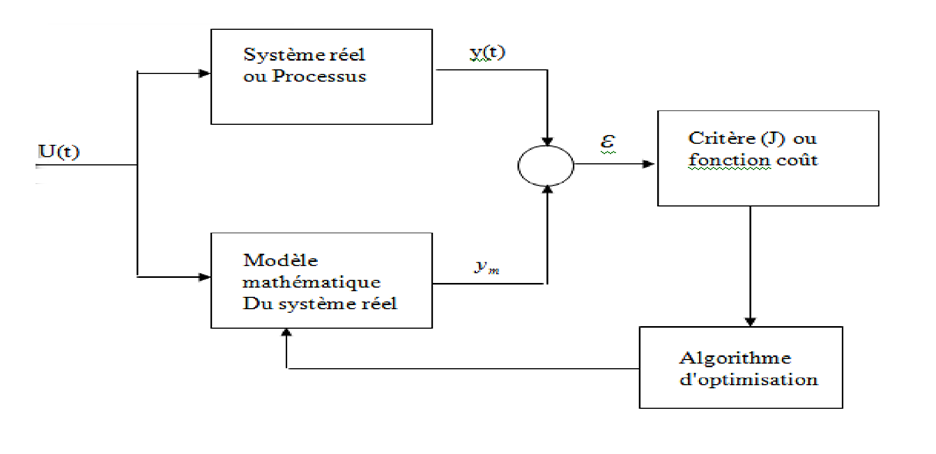

Il est important de souligner qu’il n’ y a pas un algorithme d’estimation paramétrique unique pour tous les types de modèles de bruit fournit des estimations paramétriques asymptotiquement non biaisées. Pour chaque structure de bruit, il existe des algorithmes spécifiques permettant d’obtenir des bons résultats , il convient tout d’abord de préciser les
principaux  modèles « Système + perturbation » .

L’erreur de prédiction, qui est l’erreur entre la sortie du système et celle prédite par le modèle, est utilisée par un algorithme d’adaptation paramétrique, qui à chaque instant  d’échantillonnage, va modifier les paramètres du modèle afin d’en minimiser l’erreur suivant un critère. La méthode des moindres carrés a été introduite par Karl Gauss en 1809. Elle a été à la base de toutes les méthodes d’identification et d’estimation des paramètres, cette méthode est basée sur la minimisation d’une fonction quadratique J définie comme :

II Méthode des moindres carrés

Soit le système représenté par le modèle suivant :

Modèle du système étudié

La mise en équation du système donne :

Avec u(k) et y(k) séquences d’entrée  et de sortie, B(k) bruit de mesure, k l’instant d’échantillonnage, A(z^-1) et B(z^-1) deux polynômes qui s’écrivent :  

On définit :

le vecteur des paramètres du modèle. Si on néglige le bruit de mesure et si on possède  N  mesures consécutives (u, y), on peut écrire N − n fois l’équation (2). Soit :

Alors :

Le critère J est :

avec 

les résidus d’estimation. Donc :

On cherche la valeur   qui minimise J . Ainsi:

D’où on en déduit l’estimateur du vecteur des paramètres :