1.1.4.4. Architecture des mémoires centrales
Dans une architecture à un seul processeur : le processeur à l’exclusivité d’accéder à la mémoire. Le rendement de l’UC n’est conditionné que par le temps d’accès à la MC.
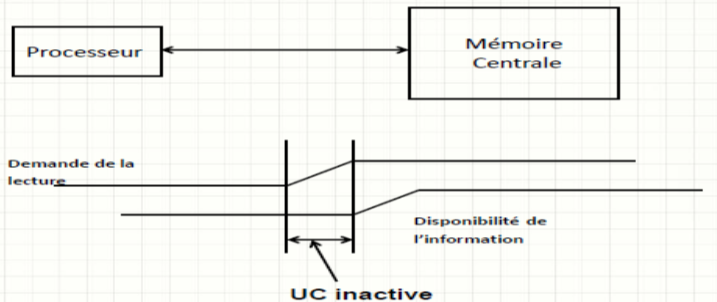
Figure 1.4. Interaction processeur – Mémoire centrale
Si le calculateur possède plusieurs processeurs qui fonctionnent en parallèle (en même temps), c’est possible que deux processeurs ou plus demandent d’accéder à la mémoire à la même instant.
Si la mémoire est structurée en un seul bloc alors un processeur peut monopoliser la MC. Même si le temps d’accès est très petit, des processeurs vont être pénalisés ⇒ donc la structure de la MC est aussi importante.
Solutions :
a-) Mémoire modulaire
- La solution est de découper la mémoire centrale en plusieurs modules.
- Plusieurs bus permettent d’accéder simultanément (en même temps) à la MC.
- Possible d’avoir autant d’accès que de modules.
- On ne peut pas accéder simultanément à un module.

Remarque :
- Les adresses à l’intérieur d’un module sont séquentiels (successives)
- C’est possible qu’un module soit réaliser avec des boîtiers de taille inférieur, il faut calculer les facteur d’extension lignes et colonnes)
Sélectionner un mot dans une architecture modulaire
L’adresse est divisée en deux parties :
- Les bits de poids forts pour sélectionner un module. Si le nombre de module est égale à n , alors il faut prendre k bits tel que 2k >= n
Les bits de poids faibles pour sélectionner un mot dans un module.
![]()
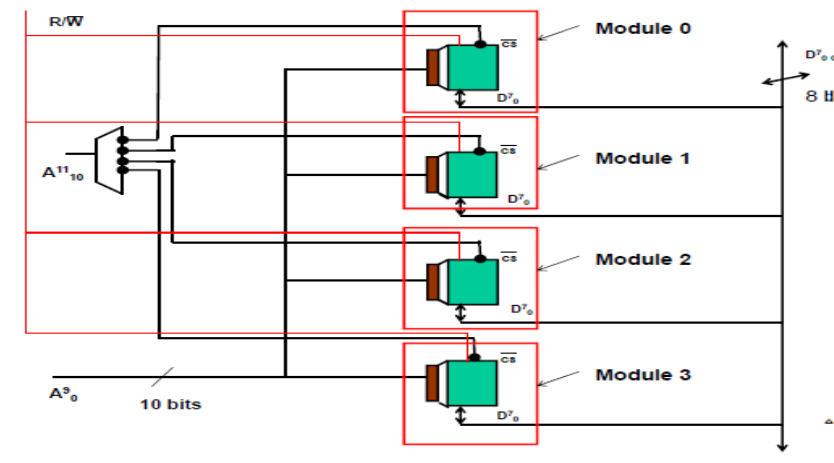
Exemple 1.3 : Soit une mémoire de taille de 4 Kmot (taille d’un mot est de 8 bits). Cette mémoire est découpée en 4 modules. Donner le schéma de cette mémoire en utilisant des boîtiers de 1 Ko?
Solution :
Capacité = 4 Kmot = 4* 210 = 212 à la taille du bus d’adresses est de 12 bits ( A110).
4 modules à 2 bits du poids forts pour la sélection des modules ( A1110)
Les autres bits pour la sélection d’un mot dans un module ( A90)
b-) Mémoire entrelacée
Avec une MC modulaire, c’est possible qu’un processeur monopolise un module (par exemple il accède à des adresses consécutives), Pour éviter ce problème :
• Un module est divisé en plusieurs Blocs.
• les adresses consécutives sont placées dans des blocs différents.
• Le nombre de blocs représente le degré d’entrelacement.
Sélectionner un mot dans une MC entrelacée
L’adresse est divisée en deux parties :
· Les bits de poids faibles pour sélectionner le bloc. Si on dispose de n bloc, il faut prendre k bits tel que 2k>=n.
· Les bits de poids forts pour sélectionner le mot dans le bloc.

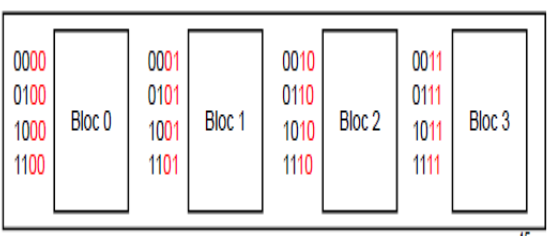
Exemple 1.4 : une mémoire entrelacée avec un degré d’entrelacement égale à 4 , un bloc est de taille de 4 mots de 4 bits.
• 4 blocs et la taille d’un bloc est égale à 4 mots de 4 bits à taille de la mémoire est égale à 16 mots de 4 bits.
• Il existe 4 blocs à 2 bits de poids faibles pour la sélection A10
• Les bits de poids forts ( A32) pour sélectionner un mot dans un bloc.
• L’adresse 0000 à bloc 0 ( bits poids faible 00)
• L’adresse 0001 à bloc 1 ( bits poids faible 01)
• L’adresse 0010 à Bloc 2
• L’adresse 0011 à Bloc 3
• L’adresse 0100 à Bloc 0
• ………..
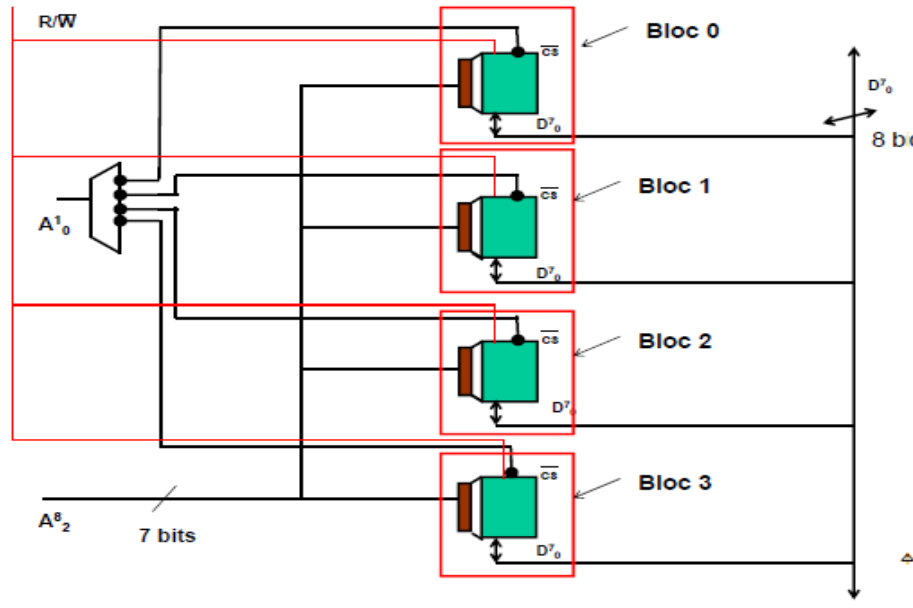
Exemple 1.5 : Réaliser une mémoire de capacité 512 mots de 8 bits avec des boîtiers de 128 mots de 8 bits avec un degré entrelacement de 4.
- Capacité 512 =29 ( taille de bus d’adresses =9 )
- Taille d’un mot =8 à taille du bus de données =8
- 4 blocs à taille d’un bloc = 512/4 =128
- Taille d’un boîtier = 128 mots de 8 bits à un boîtier par bloc est suffisant
- 2 bits de poids faibles pour la sélection d’un bloc A10
Les bits de poids fort ( A82) pour sélectionner un mot dans un bloc.
c-) Les mémoires modulaires entrelacées
• La MC est divisée en plusieurs modules
• Chaque module est divisé en n Blocs (n le degré d’entrelacement)
• Pour sélectionner un mot :
– Il faut sélectionner le module (bits de poids forts)
– Sélectionner le bloc dans le module (bits de poids faibles)
– Sélectionner le mot dans le bloc (les bits restant)

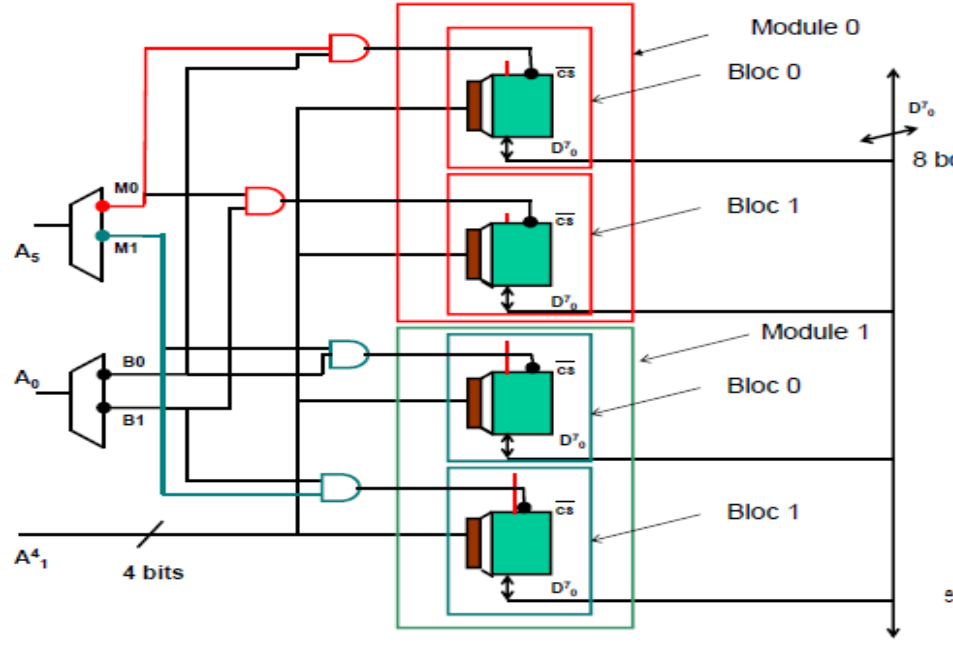
Exemple 1.6: Réaliser une mémoire de 64 mots de 8 bits organisé en deux modules entrelacé, l’entrelacement se fait à l’intérieur ( D=2). En utilisant des circuits (boîtiers) de 16 mots de 8 bits.
- La taille du bus d’adresses k= 6 ( 64=26) à A50
- Le nombre de module m=2 , la taille d’un module est égale à 32 mots.
- Le nombre de bits pour sélectionner un module est égale à 1 (A5 ).
- Le nombre de blocs dans un module D=2 à le nombre de bits nécessaire pour sélectionner un bloc est égale à 1 (A0 )
- la taille d’un bloc est égale 16 mots à un circuit suffit pour réaliser un bloc
- Le nombre de bits nécessaire pour sélectionner une mot dans le bloc est égale à 4 (A41 )