Trie par fusion :

Le tri par fusionL'algorithme est un algorithme de tri qui est considéré comme un exemple de la stratégie diviser pour mieux régner. Ainsi, dans cet algorithme, le tableau est initialement divisé en deux moitiés égales, puis elles sont combinées de manière triée. Nous pouvons le considérer comme un algorithme récursif qui divise continuellement le tableau en deux jusqu'à ce qu'il ne puisse plus être divisé. Cela signifie que si le tableau devient vide ou n'a plus qu'un seul élément, la division s'arrêtera, c'est-à-dire que c'est le cas de base pour arrêter la récursivité. Si le tableau a plusieurs éléments, nous divisons le tableau en moitiés et invoquons de manière récursive le tri par fusion sur chacune des moitiés. Enfin, lorsque les deux moitiés sont triées, l'opération de fusion est appliquée. L'opération de fusion est le processus consistant à prendre deux tableaux triés plus petits et à les combiner pour en faire éventuellement un plus grand.

Déclarez la variable gauche à 0 et la variable droite à n-1
• Trouver la formule moyenne par moyenne. milieu = (gauche+droite)/2
• Appeler le tri par fusion activé (gauche, milieu)
• Trier par fusion d'appels activé (milieu +1, arrière)
• Continuer jusqu'à ce que la gauche soit inférieure à la droite
• Appelez ensuite la fonction de fusion pour effectuer le tri par fusion.

Algorithme:

étape 1 : commencer
étape 2: déclarer un tableau et une variable gauche, droite, milieu
étape 3 : exécuter la fonction de fusion.
        fusionner (tableau, gauche, droite)
        mergesort (tableau, gauche, droite)
        si gauche > droite
        revenir
        milieu= (gauche+droite)/2
        mergesort(tableau, gauche, milieu)
        mergesort(tableau, mi+1, droite)
        fusionner (tableau, gauche, milieu, droite)
étape 4 : Arrêtez

Voir l'implémentation C suivante pour plus de détails.

FusionTrie(arr[], l, r)

Si r > l

• Trouvez le point médian pour diviser le tableau en deux moitiés : 
  • milieu m = l + (r – l)/2
• Appelez mergeSort pour la première moitié :   
  • Appelez mergeSort(arr, l, m)
• Appelez mergeSort pour la seconde moitié :
  • Appelez mergeSort(arr, m + 1, r)
• Fusionnez les deux moitiés triées aux étapes 2 et 3 :
• Appeler la fusion (arr, l, m, r)

Comment fonctionne le tri par fusion ?

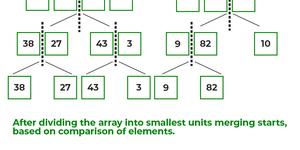
Pour connaître le fonctionnement du tri par fusion, considérons un tableau arr[] = {38, 27, 43, 3, 9, 82, 10}

• Dans un premier temps, vérifiez si l'index gauche du tableau est inférieur à l'index droit, si oui, calculez son point médian

• Maintenant, comme nous le savons déjà, le tri par fusion divise d'abord l'ensemble du tableau de manière itérative en moitiés égales, à moins que les valeurs atomiques ne soient atteintes. 
• Ici, nous voyons qu'un tableau de 7 éléments est divisé en deux tableaux de taille 4 et 3 respectivement.

• Maintenant, trouvez à nouveau que l'index de gauche est inférieur à l'index de droite pour les deux tableaux, s'il est trouvé oui, puis calculez à nouveau les points médians pour les deux tableaux.

• Maintenant, divisez davantage ces deux tableaux en deux moitiés supplémentaires, jusqu'à ce que les unités atomiques du tableau soient atteintes et qu'une division supplémentaire ne soit plus possible.

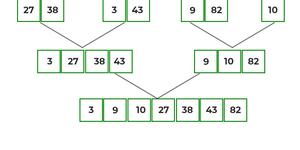
• Après avoir divisé le tableau en plus petites unités, recommencez à fusionner les éléments en fonction de la comparaison de la taille des éléments
• Tout d'abord, comparez l'élément de chaque liste, puis combinez-les dans une autre liste de manière triée.

• Après la fusion finale, la liste ressemble à ceci :

Reportez-vous aux illustrations ci-dessous pour plus de clarté :

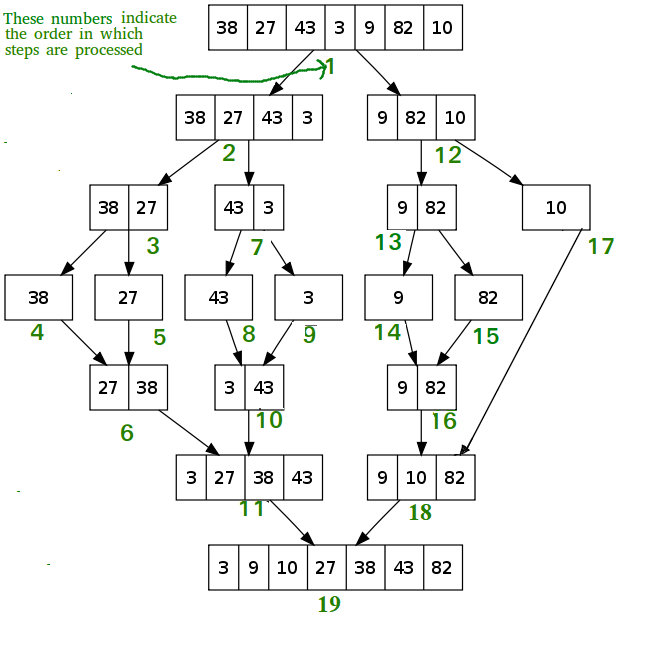
Le diagramme suivant montre le processus complet de tri par fusion pour un exemple de tableau {38, 27, 43, 3, 9, 82, 10}

Si nous examinons de plus près le diagramme, nous pouvons voir que le tableau est divisé récursivement en deux moitiés jusqu'à ce que la taille devienne

• Une fois que la taille devient 1, les processus de fusion entrent en action et commencent à fusionner les tableaux jusqu'à ce que le tableau complet soit fusionné.

void merge(int arr[], int l, int m, int r)

{

    int i, j, k;

    int n1 = m - l + 1;

    int n2 = r - m;

 

    /* create temp arrays */

    int L[n1], R[n2];

 

    /* Copy data to temp arrays L[] and R[] */

    for (i = 0; i < n1; i++)

        L[i] = arr[l + i];

    for (j = 0; j < n2; j++)

        R[j] = arr[m + 1 + j];

 

    /* Merge the temp arrays back into arr[l..r]*/

    i = 0; // Initial index of first subarray

    j = 0; // Initial index of second subarray

    k = l; // Initial index of merged subarray

    while (i < n1 && j < n2) {

        if (L[i] <= R[j]) {

            arr[k] = L[i];

            i++;

        }

        else {

            arr[k] = R[j];

            j++;

        }

        k++;

    }

 

    /* Copy the remaining elements of L[], if there

    are any */

    while (i < n1) {

        arr[k] = L[i];

        i++;

        k++;

    }

 

    /* Copy the remaining elements of R[], if there

    are any */

    while (j < n2) {

        arr[k] = R[j];

        j++;

        k++;

    }

}

 

/* l is for left index and r is right index of the

sub-array of arr to be sorted */

void mergeSort(int arr[], int l, int r)

{

    if (l < r) {

        // Same as (l+r)/2, but avoids overflow for

        // large l and h

        int m = l + (r - l) / 2;

 

        // Sort first and second halves

        mergeSort(arr, l, m);

        mergeSort(arr, m + 1, r);

 

        merge(arr, l, m, r);

    }

}

 

/* UTILITY FUNCTIONS */

/* Function to print an array */

void printArray(int A[], int size)

{

    int i;

    for (i = 0; i < size; i++)

        printf("%d ", A[i]);

    printf("\n");

}

 

/* Driver code */

int main()

{

    int arr[] = { 12, 11, 13, 5, 6, 7 };

    int arr_size = sizeof(arr) / sizeof(arr[0]);

 

    printf("Given array is \n");

    printArray(arr, arr_size);

 

    mergeSort(arr, 0, arr_size - 1);

 

    printf("\nSorted array is \n");

    printArray(arr, arr_size);

    return 0;

}

Complexité temporelle : O(n log), Tri des tableaux sur différentes machines. Merge Sort est un algorithme récursif et la complexité temporelle peut être exprimée comme une relation de récurrence suivante. 

T = 2T(n/2) + θ

La récurrence ci-dessus peut être résolue soit à l'aide de la méthode Recurrence Tree, soit de la méthode Master. Il tombe dans le cas II de la méthode maître et la solution de la récurrence est θ(nLogn). La complexité temporelle du tri par fusion est θ(nLogn) dans les 3 cas (pire, moyen et meilleur) car le tri par fusion divise toujours le tableau en deux moitiés et prend un temps linéaire pour fusionner les deux moitiés.
Espace auxiliaire : OComplexité spatiale :• Dans le tri par fusion, tous les éléments sont copiés dans un tableau auxiliaire 
• donc N espace auxiliaire est requis pour le tri par fusion.
 Paradigme algorithmique : diviser pour mieux régner

Le tri par fusion est-il en place ?

 Non dans une implémentation typique

Le tri par fusion est-il stable : 

Oui, le tri par fusion est stable. 

Applications du tri par fusion : 

• Le tri par fusion est utile pour trier les listes chaînées en temps O(nLogn) . Dans le cas des listes chaînées, le cas est différent principalement en raison de la différence d'allocation de mémoire des tableaux et des listes chaînées. Contrairement aux tableaux, les nœuds de liste chaînée peuvent ne pas être adjacents en mémoire. Contrairement à un tableau, dans la liste chaînée, nous pouvons insérer des éléments au milieu dans un espace supplémentaire O (1) et un temps O (1). Par conséquent, l'opération de fusion du tri par fusion peut être implémentée sans espace supplémentaire pour les listes chaînées.
  Dans les tableaux, nous pouvons faire un accès aléatoire car les éléments sont contigus en mémoire. Disons que nous avons un tableau d'entiers (4 octets) A et que l'adresse de A[0] soit x puis pour accéder à A[i], nous pouvons accéder directement à la mémoire à (x + i*4). Contrairement aux tableaux, nous ne pouvons pas faire d'accès aléatoire dans la liste chaînée. Le tri rapide nécessite beaucoup de ce type d'accès. Dans une liste chaînée pour accéder au iième index, nous devons parcourir chaque nœud de la tête au iième nœud car nous n'avons pas de bloc de mémoire contigu. Par conséquent, la surcharge augmente pour le tri rapide. Le tri par fusion accède aux données de manière séquentielle et le besoin d'accès aléatoire est faible.

Inconvénients du tri par fusion :

• Plus lent par rapport aux autres algorithmes de tri pour les tâches plus petites.
• L'algorithme de tri par fusion nécessite un espace mémoire supplémentaire de 0 pour le tableau temporaire.
• Il parcourt tout le processus même si le tableau est trié.