comme Merge Sort , QuickSort est un algorithme Divide and Conquer . Il sélectionne un élément comme pivot et partitionne le tableau donné autour du pivot sélectionné. Il existe de nombreuses versions différentes de quickSort qui sélectionnent le pivot de différentes manières. 

• Choisissez toujours le premier élément comme pivot.
• Choisissez toujours le dernier élément comme pivot (implémenté ci-dessous)
• Choisissez un élément aléatoire comme pivot.
• Choisissez la médiane comme pivot.

Le processus clé dans quickSort est une partition(). La cible des partitions est, étant donné un tableau et un élément x d'un tableau comme pivot, mettre x à sa position correcte dans un tableau trié et mettre tous les éléments plus petits (plus petit que x) avant x, et mettre tous les éléments plus grands (plus grand que x) après x. Tout cela doit être fait en temps linéaire.

Algorithme de partition : 

Il peut y avoir plusieurs façons de partitionner, le pseudo-code suivant adopte la méthode donnée dans le livre CLRS. La logique est simple, nous partons de l'élément le plus à gauche et gardons une trace de l'index des éléments plus petits (ou égaux à) comme i. En parcourant, si on trouve un élément plus petit, on échange l'élément courant avec arr[i]. Sinon, nous ignorons l'élément courant. 

Pseudo-code pour la fonction récursive QuickSort :

/* bas -> Index de départ, haut -> Index de fin */

tri rapide(arr[], bas, haut) {

    si (faible < élevé) {

        /* pi est l'index de partitionnement, arr[pi] est maintenant au bon endroit */

        pi = partition(arr, bas, haut);

        tri rapide(arr, bas, pi - 1); // Avant pi

        tri rapide(arr, pi + 1, haut); // Après pi

    }

}

Pseudo-code pour partition()  

/* Cette fonction prend le dernier élément comme pivot, place l'élément pivot à sa position correcte dans un tableau trié et place tous les éléments plus petits (plus petits que pivot) à gauche du pivot et tous les éléments supérieurs à droite du pivot */

partition (arr[], bas, haut)

{

    // pivot (Elément à placer à droite)
pivot = arr[high];  

 i = (faible - 1) // Index du plus petit élément et indique la 
// bonne position du pivot trouvé jusqu'à présent

pour (j = bas ; j <= haut- 1 ; j++){

 // Si l'élément courant est plus petit que le pivot
if (arr[j] < pivot){
i++; // incrémente l'index du plus petit élément
 échange arr[i] et arr[j]
     }
 }

    échanger arr[i + 1] et arr[high])
return (i + 1)
}

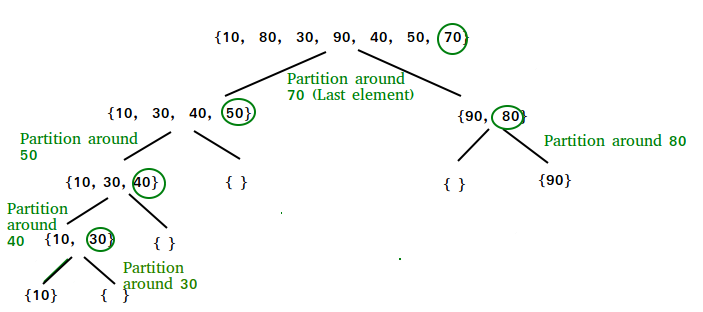
Illustration de partition() : 

Considérez : arr[] = {10, 80, 30, 90, 40, 50, 70}

• Index : 0 1 2 3 4 5 6 
• bas = 0, haut = 6, pivot = arr[h] = 70
• Initialiser l'index du plus petit élément, i = -1

• Traverser les éléments de j = bas à haut-1
  • j = 0 : Puisque arr[j] <= pivot, faire i++ et swap(arr[i], arr[j])
  • je = 0 
• arr[] = {10, 80, 30, 90, 40, 50, 70} // Pas de changement car i et j sont identiques
• j = 1 : Puisque arr[j] > pivot, ne rien faire

• j = 2 : Puisque arr[j] <= pivot, faire i++ et swap(arr[i], arr[j])
• je = 1
• arr[] = {10, 30, 80, 90, 40, 50, 70} // On échange 80 et 30 

• j = 3 : Puisque arr[j] > pivot, ne rien faire // Aucun changement dans i et arr[]
• j = 4 : Puisque arr[j] <= pivot, faire i++ et swap(arr[i], arr[j])
• je = 2
• arr[] = {10, 30, 40, 90, 80, 50, 70} // 80 et 40 échangés

• j = 5 : Puisque arr[j] <= pivot, faire i++ et échanger arr[i] avec arr[j] 
• je = 3 
• arr[] = {10, 30, 40, 50, 80, 90, 70} // 90 et 50 échangés 

• On sort de boucle car j est maintenant égal à high-1.
• Enfin, nous plaçons le pivot à la bonne position en échangeant arr[i+1] et arr[high] (ou pivot) 
• arr[] = {10, 30, 40, 50, 70, 90, 80} // 80 et 70 échangés 

• Maintenant, 70 est à sa place. Tous les éléments inférieurs à 70 sont avant et tous les éléments supérieurs à 70 sont après.
• Étant donné que le tri rapide est une fonction récursive, nous appelons à nouveau la fonction de partition sur les partitions gauche et droite

• Appelez à nouveau la fonction dans la partie droite et échangez 80 et 90

void swap(int* a, int* b) 

{ 

    int t = *a; 

    *a = *b; 

    *b = t; 

} 

  

/* This function takes last element as pivot, places 

the pivot element at its correct position in sorted 

array, and places all smaller (smaller than pivot) 

to left of pivot and all greater elements to right 

of pivot */

int partition (int arr[], int low, int high) 

{ 

    int pivot = arr[high]; // pivot 

    int i = (low - 1); // Index of smaller element and indicates the right position of pivot found so far

  

    for (int j = low; j <= high - 1; j++) 

    { 

        // If current element is smaller than the pivot 

        if (arr[j] < pivot) 

        { 

            i++; // increment index of smaller element 

            swap(&arr[i], &arr[j]); 

        } 

    } 

    swap(&arr[i + 1], &arr[high]); 

    return (i + 1); 

} 

  

/* The main function that implements QuickSort 

arr[] --> Array to be sorted, 

low --> Starting index, 

high --> Ending index */

void quickSort(int arr[], int low, int high) 

{ 

    if (low < high) 

    { 

        /* pi is partitioning index, arr[p] is now 

        at right place */

        int pi = partition(arr, low, high); 

  

        // Separately sort elements before 

        // partition and after partition 

        quickSort(arr, low, pi - 1); 

        quickSort(arr, pi + 1, high); 

    } 

} 

  

/* Function to print an array */

void printArray(int arr[], int size) 

{ 

    int i; 

    for (i = 0; i < size; i++) 

        cout << arr[i] << " "; 

    cout << endl; 

} 

  

// Driver Code

int main() 

{ 

    int arr[] = {10, 7, 8, 9, 1, 5}; 

    int n = sizeof(arr) / sizeof(arr[0]); 

    quickSort(arr, 0, n - 1); 

    cout << "Sorted array: \n"; 

    printArray(arr, n); 

    return 0; 

} 

Analyse de QuickSort 

Le temps pris par QuickSort, en général, peut être écrit comme suit. 

 T = T(k) + T(nk-1) +  

Les deux premiers termes sont pour deux appels récursifs, le dernier terme est pour le processus de partition. k est le nombre d'éléments qui sont plus petits que le pivot. 
Le temps pris par QuickSort dépend du tableau d'entrée et de la stratégie de partition. Voici trois cas.

Pire cas : 
le pire des cas se produit lorsque le processus de partition sélectionne toujours l'élément le plus grand ou le plus petit comme pivot. Si nous considérons la stratégie de partition ci-dessus où le dernier élément est toujours choisi comme pivot, le pire des cas se produirait lorsque le tableau est déjà trié par ordre croissant ou décroissant. Voici la récurrence pour le pire des cas.  

 T = T(0) + T(n-1) +  ce qui équivaut à T = T(n-1) +  

La solution de la récurrence ci-dessus est   (n 2 ). 

Meilleur cas :
le meilleur cas se produit lorsque le processus de partition choisit toujours l'élément du milieu comme pivot. Ce qui suit est la récurrence pour le meilleur des cas. 

 T = 2T(n/2) +