Recherche Fibonacci
Soit un tableau trié arr[] de taille n et un élément x à rechercher dedans. Renvoie l'index de x s'il est présent dans le tableau sinon renvoie -1.
Exemples:
Entrée : tab[] = {2, 3, 4, 10, 40}, x = 10 Sortie : 3 L'élément x est présent à l'indice 3. Entrée : tab[] = {2, 3, 4, 10, 40}, x = 11 Sortie : -1 L'élément x n'est pas présent.
La recherche de Fibonacci est une technique basée sur la comparaison qui utilise les nombres de Fibonacci pour rechercher un élément dans un tableau trié.
Similitudes avec la recherche binaire :
- Fonctionne pour les tableaux triés
- Un algorithme Diviser pour mieux régner.
- A une complexité de temps Log n.
Différences avec la recherche binaire :
- La recherche de Fibonacci divise un tableau donné en parties inégales
- La recherche binaire utilise un opérateur de division pour diviser la plage. Fibonacci Search n'utilise pas /, mais utilise + et -. L'opérateur de division peut être coûteux sur certains processeurs.
- Fibonacci Search examine des éléments relativement plus proches dans les étapes suivantes. Ainsi, lorsque le tableau d'entrée est grand et ne peut pas tenir dans le cache du processeur ou même dans la RAM, la recherche Fibonacci peut être utile.
Contexte :
Les nombres de Fibonacci sont définis de manière récursive comme F = F(n-1) + F(n-2), F(0) = 0, F(1) = 1. Les premiers nombres de Fibonacci sont 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Observations :
L'observation ci-dessous est utilisée pour l'élimination de la plage, et donc pour la complexité O(log).
F(n - 2) ≥ (1/3)*F(n) et F(n - 1) ≥ (2/3)*F(n).
Algorithme :
Soit x pour l'élément recherché.
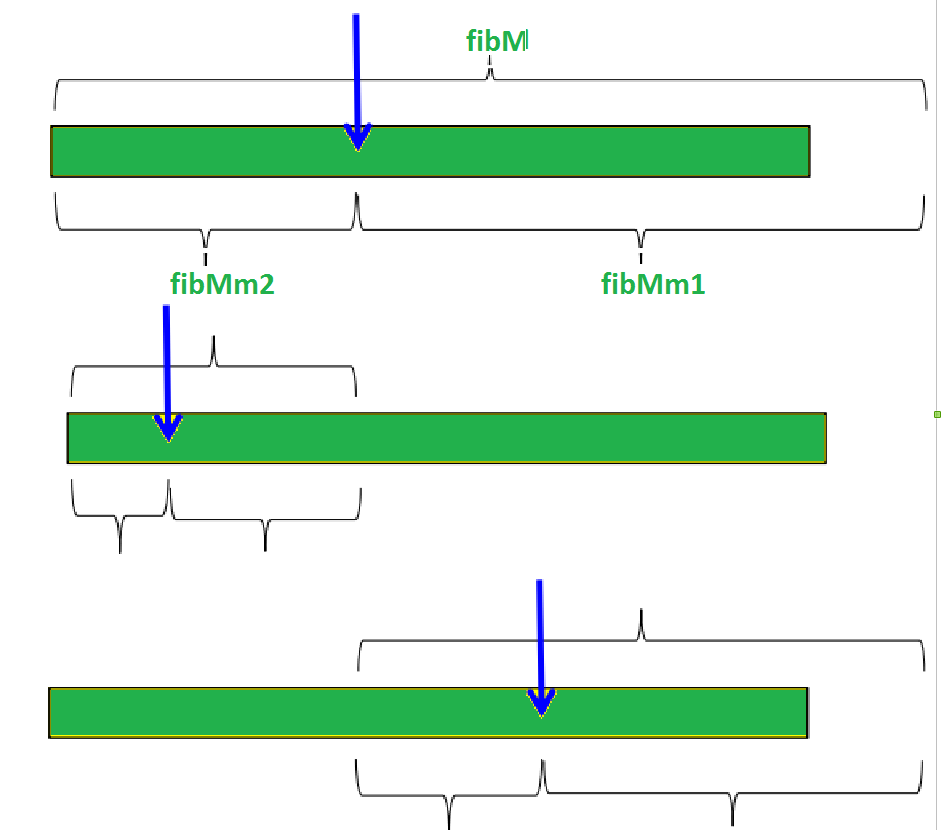
L'idée est de trouver d'abord le plus petit nombre de Fibonacci supérieur ou égal à la longueur du tableau donné. Soit le nombre de Fibonacci trouvé fib (m'ième nombre de Fibonacci). Nous utilisons le (m-2)ème nombre de Fibonacci comme indice (s'il s'agit d'un indice valide). Soit (m-2)'ème nombre de Fibonacci soit i, nous comparons arr[i] avec x, si x est identique, nous renvoyons i. Sinon, si x est plus grand, on revient pour le sous-tableau après i, sinon on revient pour le sous-tableau avant i.
Ci-dessous l'algorithme complet
Soit arr[0..n-1] le tableau d'entrée et l'élément à rechercher soit x.
- Trouver le plus petit nombre de Fibonacci supérieur ou égal à n. Soit ce nombre fibM [m'ième nombre de Fibonacci]. Soit les deux nombres de Fibonacci qui le précèdent fibMm1 [(m-1)'ème nombre de Fibonacci] et fibMm2 [(m-2)'ème nombre de Fibonacci].
- Alors que le tableau a des éléments à inspecter :
- Comparer x avec le dernier élément de la plage couverte par fibMm2
- Si x correspond, renvoie l'index
- Sinon, si x est inférieur à l'élément, déplacez les trois variables de Fibonacci de deux Fibonacci vers le bas, indiquant l'élimination d'environ les deux tiers arrière du tableau restant.
- Sinon x est supérieur à l'élément, déplacez les trois variables de Fibonacci d'un Fibonacci vers le bas. Réinitialiser le décalage à l'index. Ensemble, ceux-ci indiquent l'élimination d'environ un tiers avant du réseau restant.
- Puisqu'il peut rester un seul élément à comparer, vérifiez si fibMm1 vaut 1. Si oui, comparez x avec cet élément restant. Si match, retourne l'index
int min(int x, int y) { return (x <= y) ? x : y; } /* Returns index of x if present, else returns -1 */int fibMonaccianSearch(int arr[], int x, int n){ /* Initialize fibonacci numbers */ int fibMMm2 = 0; // (m-2)'th Fibonacci No. int fibMMm1 = 1; // (m-1)'th Fibonacci No. int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci /* fibM is going to store the smallest Fibonacci Number greater than or equal to n */ while (fibM < n) { fibMMm2 = fibMMm1; fibMMm1 = fibM; fibM = fibMMm2 + fibMMm1; } // Marks the eliminated range from front int offset = -1; /* while there are elements to be inspected. Note that we compare arr[fibMm2] with x. When fibM becomes 1, fibMm2 becomes 0 */ while (fibM > 1) { // Check if fibMm2 is a valid location int i = min(offset + fibMMm2, n - 1); /* If x is greater than the value at index fibMm2, cut the subarray array from offset to i */ if (arr[i] < x) { fibM = fibMMm1; fibMMm1 = fibMMm2; fibMMm2 = fibM - fibMMm1; offset = i; } /* If x is greater than the value at index fibMm2, cut the subarray after i+1 */ else if (arr[i] > x) { fibM = fibMMm2; fibMMm1 = fibMMm1 - fibMMm2; fibMMm2 = fibM - fibMMm1; } /* element found. return index */ else return i; } /* comparing the last element with x */ if (fibMMm1 && arr[offset + 1] == x) return offset + 1; /*element not found. return -1 */ return -1;} /* driver function */int main(void){ int arr[] = { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100,235}; int n = sizeof(arr) / sizeof(arr[0]); int x = 235; int ind = fibMonaccianSearch(arr, x, n); if(ind>=0) printf("Found at index: %d",ind); else printf("%d isn't present in the array",x); return 0;}Comprenons l'algorithme avec l'exemple ci-dessous :

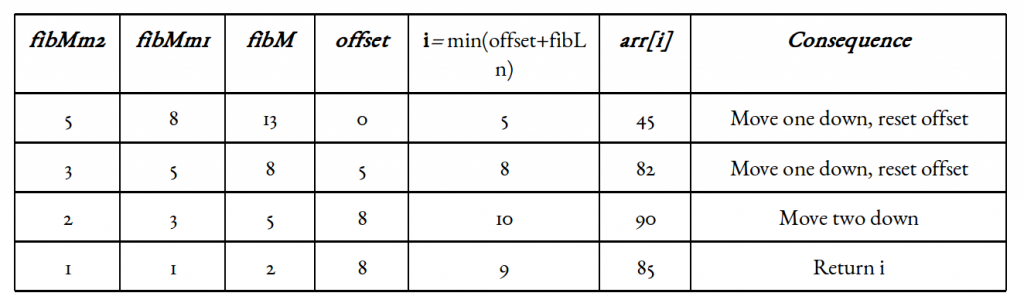
plus petit nombre de Fibonacci supérieur ou égal à 11 est 13. Selon notre illustration, fibMm2 = 5, fibMm1 = 8 et fibM = 13.
Un autre détail de mise en œuvre est la variable de décalage (initialisé à zéro). Il marque la plage qui a été éliminée, en commençant par l'avant. Nous le mettrons à jour de temps à autre.
Maintenant, puisque la valeur de décalage est un index et que tous les index l'incluant et en dessous ont été éliminés, il est logique d'y ajouter quelque chose. Étant donné que fibMm2 marque environ un tiers de notre tableau, ainsi que les indices qu'il marque, sont sûrs d'être valides, nous pouvons ajouter fibMm2 à offset et vérifier l'élément à l'indice i = min(offset + fibMm2, n).
Analyse de la complexité temporelle :
le pire des cas se produira lorsque nous aurons notre cible dans la plus grande fraction (2/3) du tableau, au fur et à mesure que nous la trouverons. En d'autres termes, nous éliminons à chaque fois la plus petite fraction (1/3) du tableau. Nous appelons une fois pour n, puis pour (2/3) n, puis pour (4/9) n, et désormais.
Considérez que :


