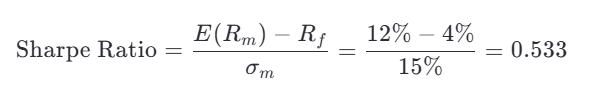Lecture 6: The Efficient Frontier and Efficient Portfolios

---

1. Concept of the Efficient Frontier

The Efficient Frontier is a graphical representation of portfolios that offer the highest expected return for a given level of risk or the lowest risk for a given level of expected return. It represents the set of optimal portfolios that maximize returns for varying levels of risk.

• Key Characteristics :

  • Portfolios on the efficient frontier are considered "efficient" because they provide the best possible trade-off between risk and return.
  • Portfolios below the efficient frontier are suboptimal as they either offer lower returns for the same level of risk or higher risk for the same level of return.
   

• Graphical Representation :

  • The x-axis represents portfolio risk (standard deviation).
  • The y-axis represents portfolio return.
  • The efficient frontier is a curved line that starts from the minimum variance portfolio and extends upward, indicating increasing returns with increasing risk.

---

2. Identifying Efficient Portfolios

Efficient portfolios are those that satisfy one of the following conditions:

1. Maximum Return for a Given Level of Risk :
   For a specific level of risk (σp​), an efficient portfolio provides the highest possible return (E(Rp​)).

2. Minimum Risk for a Given Level of Return :
   For a specific level of return (E(Rp​)), an efficient portfolio minimizes the risk (σp​).

• Optimization Process :
  To identify efficient portfolios, investors use mathematical optimization techniques to solve for weights (wi​) that maximize return or minimize risk under constraints such as:

                                                   

---

3. Utility Curves and Their Impact on Optimal Portfolio Selection

Utility Curves represent an investor's preferences for risk and return. Each curve corresponds to a specific level of utility (satisfaction) for the investor, based on their risk tolerance.

• Key Points :

  • Investors aim to select a portfolio that maximizes their utility.
  • The optimal portfolio lies at the point where the investor's utility curve is tangent to the efficient frontier.
  • More risk-averse investors will choose portfolios closer to the minimum variance portfolio, while less risk-averse investors will choose portfolios farther along the efficient frontier.

• Graphical Representation :

  • Utility curves are upward-sloping and convex to the x-axis.
  • The tangency point between the utility curve and the efficient frontier identifies the optimal portfolio for the investor.

---

4. Capital Market Line (CML) and Its Relationship with Efficient Portfolios and the Risk-Free Asset

The Capital Market Line (CML) is a key concept in modern portfolio theory that incorporates the risk-free asset into the efficient frontier.

• Definition :
  The CML represents all possible combinations of the risk-free asset and the market portfolio (the optimal risky portfolio). It shows the trade-off between risk and return for these combinations.

Equation of the CML :

• Key Features :

  • The slope of the CML is called the Sharpe Ratio , which measures the excess return per unit of risk.
  • The CML starts at the risk-free rate (Rf​) on the y-axis and passes through the market portfolio on the efficient frontier.
  • Portfolios along the CML dominate those below it, as they offer better risk-return trade-offs.

• Impact of the Risk-Free Asset :
  Including the risk-free asset allows investors to create leveraged portfolios (borrowing at Rf​ to invest more in the market portfolio) or conservative portfolios (lending at Rf​). This shifts the efficient frontier from a curve to a straight line (the CML).

---

5. Practical Examples and Calculations

Example 1: Identifying an Efficient Portfolio

Suppose you have two assets:

• Asset A: E(RA​)=10%, σA​=15%
• Asset B: E(RB​)=12%, σB​=20%
• Correlation (ρA,B​) = 0.5

Step 1: Calculate Portfolio Weights for Minimum Variance
Using optimization techniques, find weights wA​ and wB​ that minimize portfolio variance. Assume wA​=0.6 and wB​=0.4.

Step 2: Calculate Portfolio Return and Risk

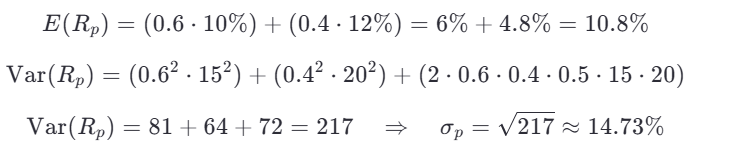
This portfolio lies on the efficient frontier.

---

Example 2: Capital Market Line

Given:

• Rf​=4%

• Market Portfolio: E(Rm​)=12%, σm​=15%

 

Step 1: Calculate Sharpe Ratio

Step 2: Determine Portfolio Return for σp​=10%

                                                                        E(Rp​)=4%+(0.533⋅10%)=4%+5.33%=9.33%

---

Key Takeaways

1. Efficient Frontier : Represents portfolios that maximize returns for a given level of risk or minimize risk for a given level of return.
2. Utility Curves : Help investors identify their optimal portfolio based on risk preferences.
3. Capital Market Line (CML) : Incorporates the risk-free asset and provides superior risk-return combinations.
4. Practical Application : Understanding these concepts enables investors to construct optimal portfolios tailored to their risk tolerance and return objectives.